Question

Найдите экстремиум функции f(x)=x²-4x

Answer 1

Ответ:

-4

Пошаговое объяснение:

Экстремум -- значение функции (у), которое является максимумом или минимумом функции.

Точка экстремума -- точка, в которой достигается максимальное или минимальное значение функции.

То есть в данном задании нужно найти минимум или максимум.

Рассмотрим уравнение: y = x² - 4x -- это квадратное уравнение, то есть его графиком будет парабола.

У параболы только одна точка экстремума: либо минимум, либо максимум, в зависимости от её коэффициента.

В данной параболе а = 1 (больше нуля), то есть коэффициент положительный (ветви параболы вверх), то есть будет точка минимума.

Эта точка будет в вершине параболы, а значит, что нам нужно найти координаты вершины.

Для этого существует формула: $x_{0} = - \frac{b}{2a}$, где x₀ -- абсцисса вершины, а а и b -- коэффициенты в уравнении (перед x² и х).

Подставим в формулу значения:

$x_{0} = - \frac{-4}{2*1} = \frac{4}{2} = 2$

Теперь найдём ординату (у) вершины, подставив полученное значение х:

y₀ = (2²) - 4 * (2) = 4 - 8 = -4

То есть вершина, или точка экстремума, находится на координатах 2;-4.

А сам экстремум -- значение у, то есть -4.

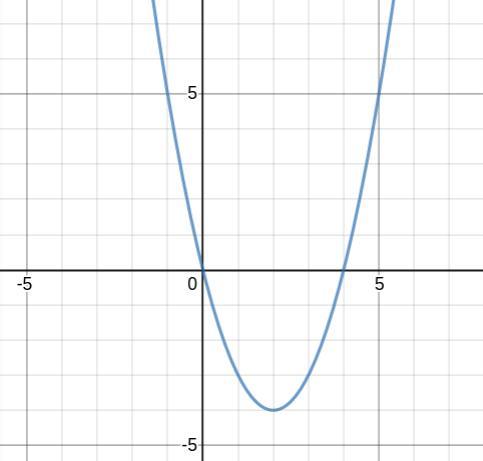
Если начертить эту параболу, то она будет выглядеть, как на прикреплённой картинке.