Question

Прошу 4 и 5, прям срочно...

Answer 1

Ответ:

4. x = 9

5. 109

Пошаговое объяснение:

4. Дано уравнение с разделяющимися переменными:

$\dfrac{dy}{dx}=\dfrac{2y^2}{3}\\\dfrac{dy}{y^2}=\dfrac{2dx}{3}\\-\dfrac{1}{y}=\dfrac{2}{3}x+C\\y=-\dfrac{1}{\frac{2}{3}x+C}$

Найдём функцию, удовлетворяющую начальному условию $x=0,y=\dfrac{1}{6}$:

$\dfrac{1}{6}=-\dfrac{1}{\frac{2}{3}\cdot 0+C}\\C=-6$

Т. е. $y=-\dfrac{1}{\frac{2}{3}x-6}$. Функция терпит разрыв, когда знаменатель равен нулю: $\dfrac{2}{3}x-6=0\Leftrightarrow x=9$. При таком x решение задачи Коши не существует.

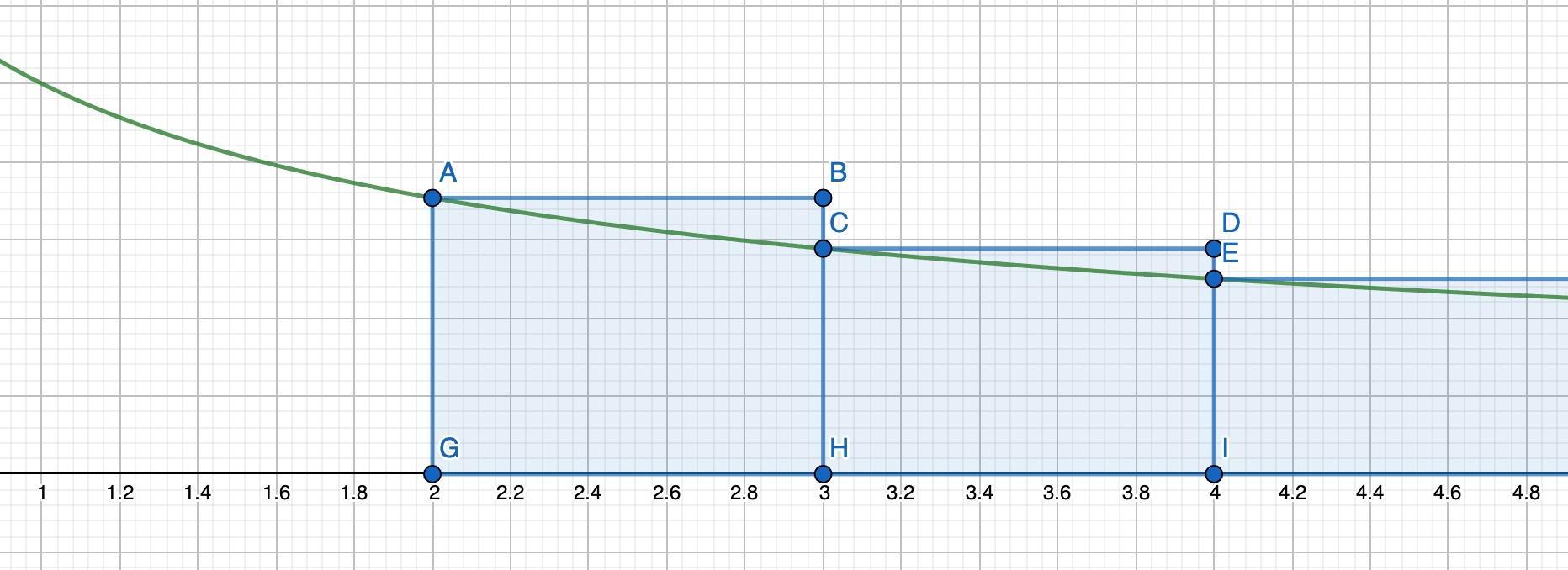
5. Рассмотрим график функции $f(x)=\dfrac{1}{\sqrt{x}}$. Геометрически искомую сумму можно представить, как сумму площадей прямоугольников с длиной 1 и шириной $\dfrac{1}{\sqrt{x}}$, где x — натуральное число от 2 до 3136. Расположим прямоугольники, как на первом рисунке. Тогда наша сумма будет больше, чем площадь под графиком функции от 2 до 3136 (по построению следовало бы считать площадь до 3137, но для простоты последующих вычислений один из кусочков площади мы просто уберём — нижняя оценка станет чуть менее точной, но незначительно), то есть $\displaystyle \sum_{n=2}^{3136} \dfrac{1}{\sqrt{n}} > \int\limits^{3136}_2 {\dfrac{dx}{\sqrt{x}}}$.

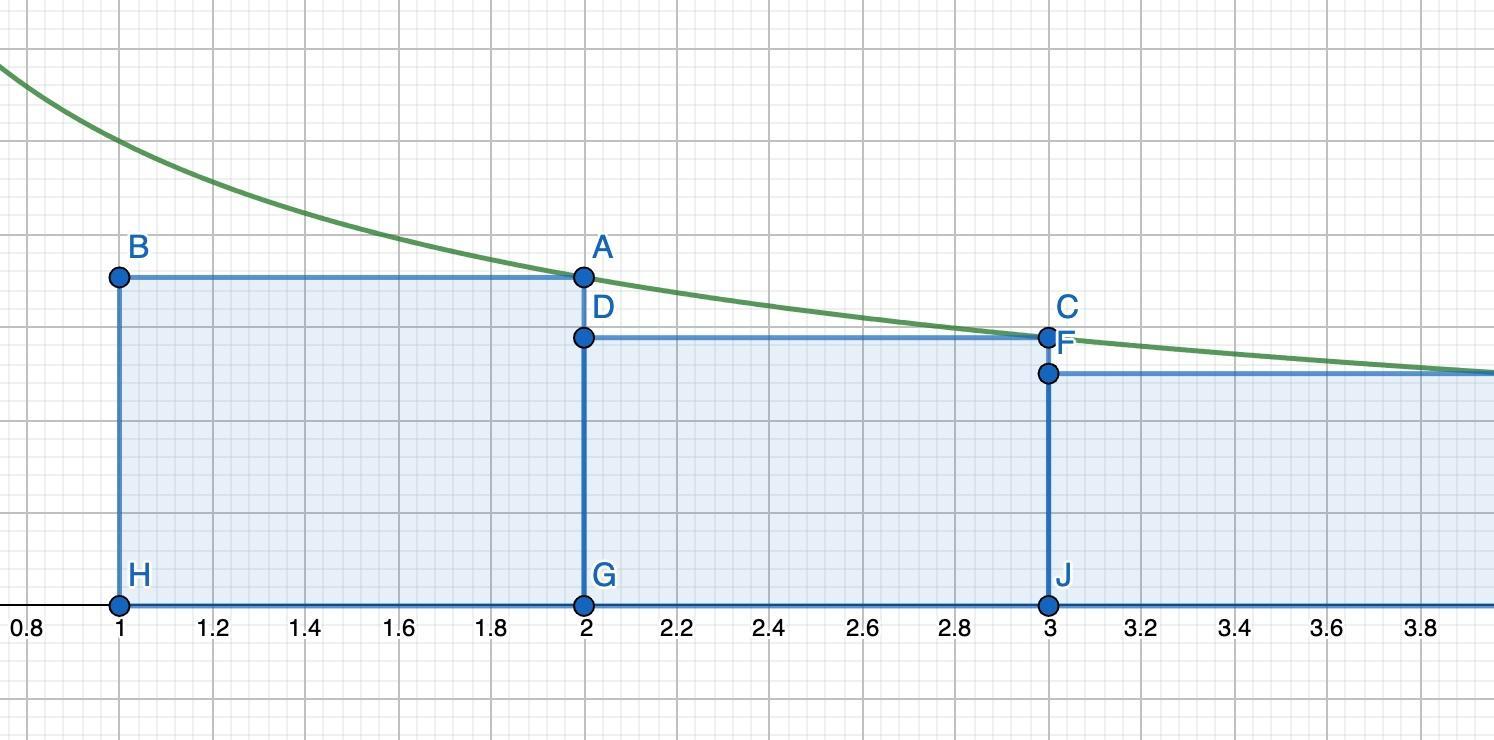
Теперь каждый прямоугольник зеркально повернём относительно их левых сторон (как на втором рисунке). Это всё та же сумма, но теперь её можно оценить сверху: площадь этих прямоугольников будет меньше, чем площадь под графиком функции от 1 до 3136): $\displaystyle \sum_{n=2}^{3136} \dfrac{1}{\sqrt{n}} < \int\limits^{3136}_1 {\dfrac{dx}{\sqrt{x}}}$.

Получаем:

$\displaystyle\int\limits^{3136}_2 {\dfrac{dx}{\sqrt{x}}} < \sum_{n=2}^{3136} \dfrac{1}{\sqrt{n}} < \int\limits^{3136}_1 {\dfrac{dx}{\sqrt{x}}}\\2\sqrt{3136}-2\sqrt{2} < \sum_{n=2}^{3136} \dfrac{1}{\sqrt{n}} < 2\sqrt{3136}-2\sqrt{1}\\112-2\sqrt{2} < \sum_{n=2}^{3136} \dfrac{1}{\sqrt{n}} < 110$

Поскольку $\sqrt{2} < 1{,}5$, то $112-2\sqrt{2} > 112-2\cdot 1{,}5=109$

Таким образом, $\displaystyle 109 < \sum_{n=2}^{3136} \dfrac{1}{\sqrt{n}} < 110$. Искомое число лежит между 109 и 110, значит, его целая часть равна 109.

P. S. Важное уточнение: такие оценки интегралами и площадями справедливы только для данной функции, поскольку она монотонно убывает (при решении этот момент стоит прописывать). В других случаях необходимо смотреть на поведение конкретной функции.