Предмет: Математика,
автор: warfacexui2
Если известно, что abcd - прямоугольник и AC = 18M, то сравните:
Длину AB и 9
Приложения:
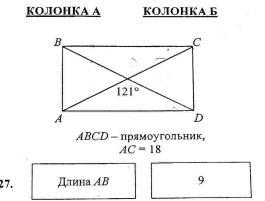
Ответы
Автор ответа:
2
Ответ:
АВ < 9
Пошаговое объяснение:
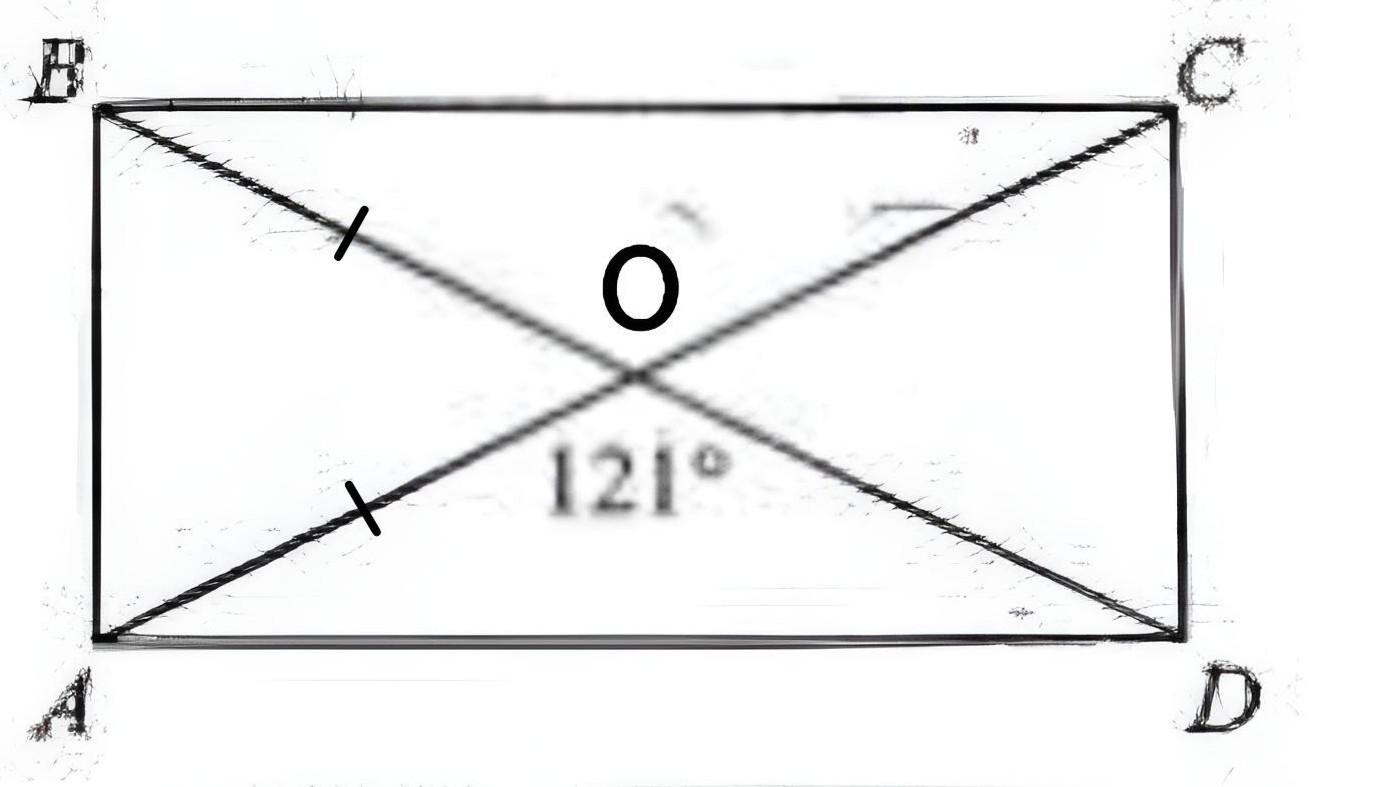
Дано: АВСD - прямоугольник , АС=18 , ∠АОD=121°
Сравнить: АВ и 9
Решение:
АС и ВD - диагонали , О - точка пересечения диагоналей , тогда ∠АОD = ∠BOC = 121° и ∠ВОА = ∠СОD (по свойству вертикальних углов) , сумму этих углов должно составить 360° , тогда ∠ВОА = ∠СОD = . Точка пересечения диагоналей делит их пополам , ВО = АО = АС : 2 = 18 : 2 = 9 , ΔВОА - равнобедренный ⇒ ∠В = ∠А , если сумма углов Δ должно составлять 180° , тогда ∠В = ∠А =
, Т.е можно сказать , нам нужно сравнить из ΔВОА основание АВ с длиной боковой стороны , можно использовать т.синусов , но лучше рассуждать , в треугольнике против меньшего угла лежит меньшая сторона , АВ лежит против меньшего ∠ВОА (59°) ⇒ АВ < 9
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: Kitilav
Предмет: Русский язык,
автор: Гюля75
Предмет: История,
автор: AngelaReu
Предмет: Биология,
автор: legalegakam