Question

помогите пожалуйста (((

Answer 1

Ответ:

$22{,}5^\circ$

Пошаговое объяснение:

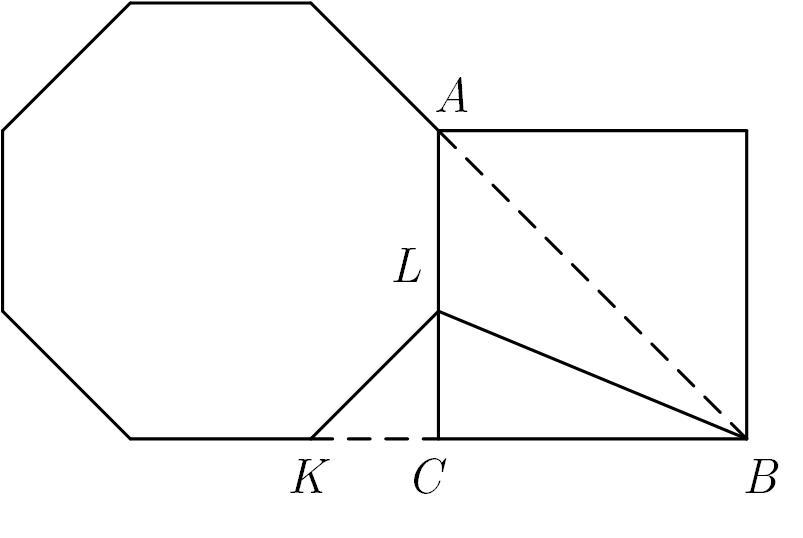
Покажем, что $BL$ — биссектриса угла $ABC$.

Так как внутренний угол правильного восьмиугольника равен

$\displaystyle\frac{{(8 - 2)180^\circ }}{8} = 135^\circ ,$

то его внешний угол $\angle KLC = \angle LKC = 180^\circ - 135^\circ = 45^\circ$. Значит треугольник $KCL$ равнобедренный прямоугольный, $KC = CL = a$, $KL = \sqrt {{a^2} + {a^2}} = a\sqrt 2$. Но $KL = LA$, поэтому

$\displaystyle\frac{{CL}}{{LA}} = \displaystyle\frac{a}{{a\sqrt 2 }} = \displaystyle\frac{1}{{\sqrt 2 }}.$

Пусть $AC = BC = x$, тогда $AB = \sqrt {{x^2} + {x^2}} = x\sqrt 2$ и

$\displaystyle\frac{{BC}}{{AB}} = \displaystyle\frac{x}{{x\sqrt 2 }} = \displaystyle\frac{1}{{\sqrt 2 }}.$

Таким образом, точка $L$ разбивает сторону $AC$ на отрезки, пропорциональные соответствующим боковым сторонам. Следовательно, $BL$ — биссектриса угла $ABC$,

$\angle LBC = \displaystyle\frac{{45^\circ }}{2} = 22{,}5^\circ .$