Предмет: Алгебра,
автор: adilabasov1987
С объяснением пожалуйста
Приложения:
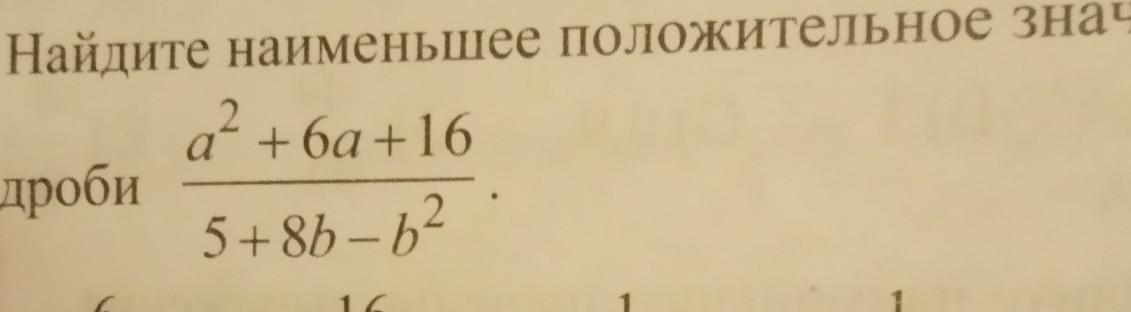
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Числитель дроби всегда больше нуля, поэтому чтобы дробь была положительной, знаменатель тоже должен быть больше нуля. При этом наименьшее значение дробь достигает, когда числитель наименьший, а знаменатель наибольший.
Так как
а
то наименьшее положительное значение дроби равно при
selfcare39:
здравствуйте, помогите пожалуйста с алгеброй задание у меня в профиле отмечу 5 звёзд и сделаю лучший ответ
Похожие вопросы
Предмет: Английский язык,
автор: vlad1126
Предмет: Українська мова,
автор: Аноним
Предмет: Технология,
автор: Qumru
Предмет: Геометрия,
автор: cashokshka
Предмет: Математика,
автор: парвина87