Question

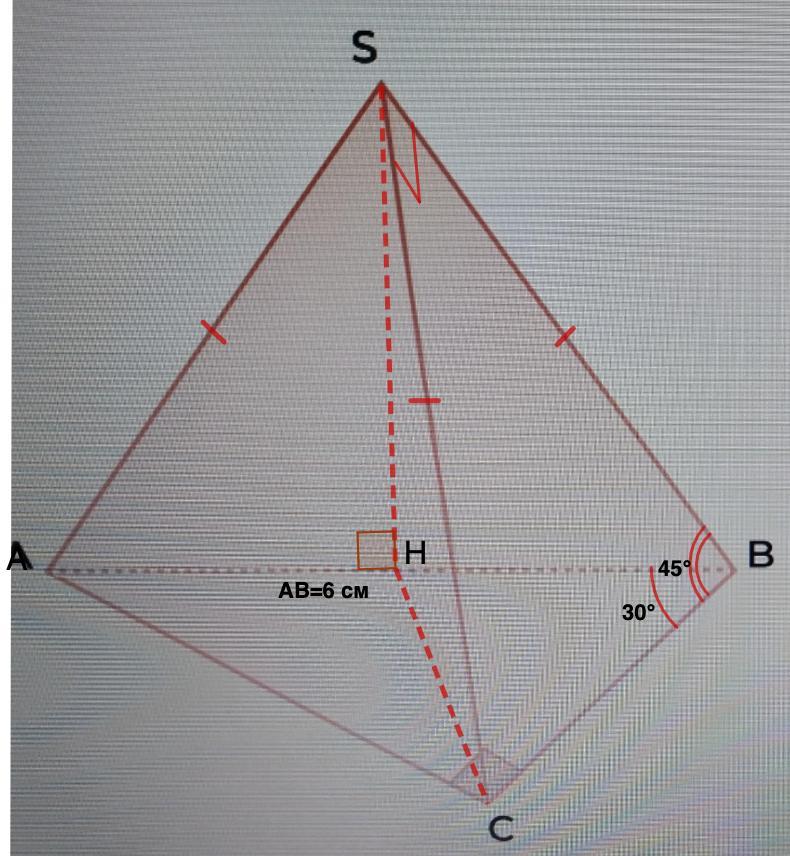
Дана пирамида SABC, угол AСB равен 90, угол ABC равен 30, угол SBC 45. AS= BS=CS, AB=6. Найти объем пирамиды

Answer 1

Ответ:

Объем пирамиды равен $\displaystyle\bf \frac{9\sqrt{6} }{4}$  см³.

Объяснение:

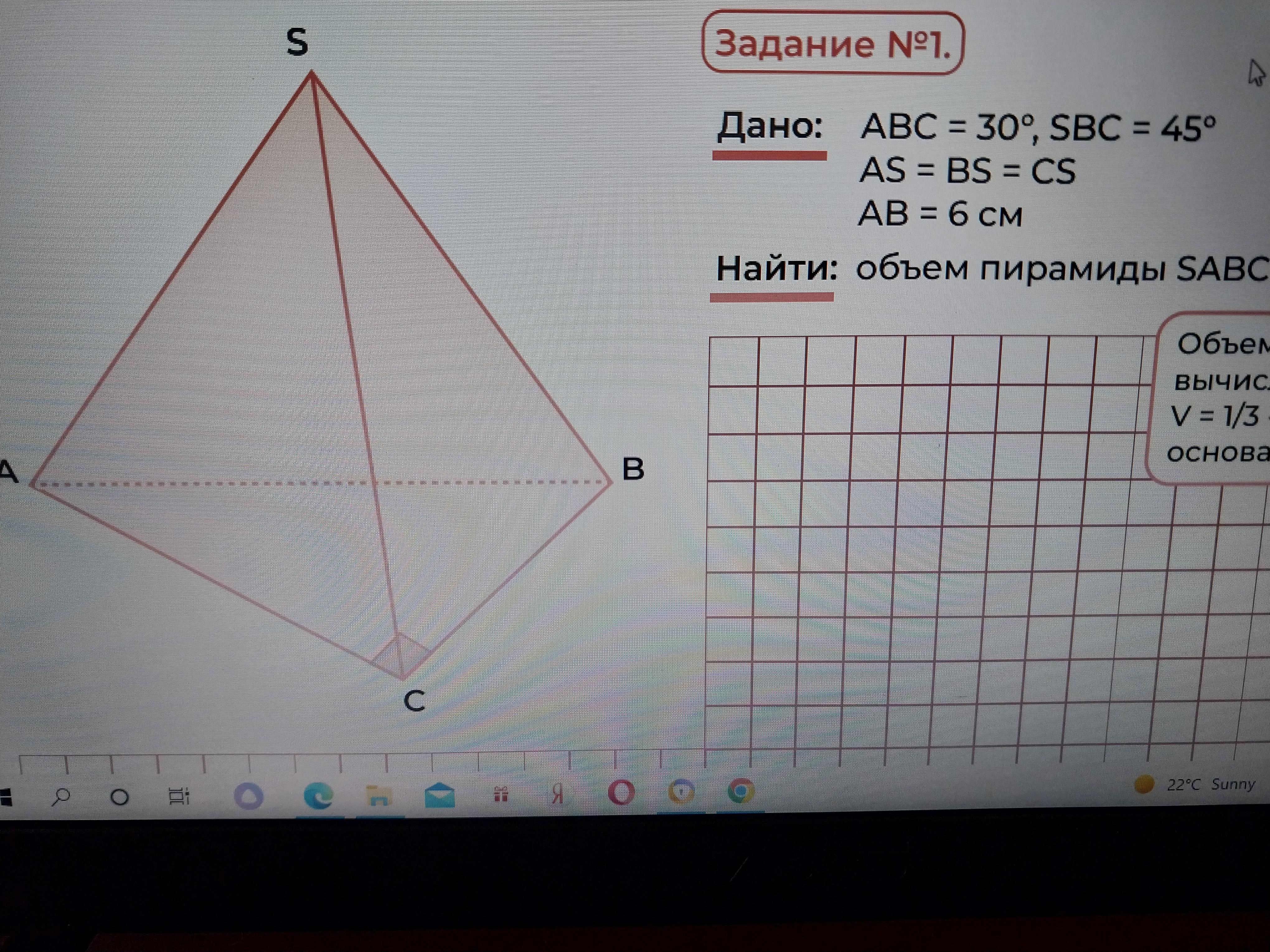
Дана пирамида SABC, угол AСB равен 90, угол ABC равен 30, угол SBC 45. AS= BS=CS, AB=6. Найти объем пирамиды.

Дано: SABC - пирамида.

SA = SB = SC;

∠ABC = 30°; ∠АСВ = 90°;

AB = 6 см.

Найти: V(SABC)

Решение:

• Объем пирамиды равен одной трети произведения площади основания на высоту:

• $\boxed {\displaystyle\bf V=\frac{1}{3}S_{OCH}\cdot{h} }$

1. Найдем площадь основания.

В основании пирамиды лежит прямоугольный треугольник.

Рассмотрим ΔАВС - прямоугольный.

АВ = 6 см.

∠АВС = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ АС = АВ : 2 = 6 : 2 = 3 (см)

По теореме Пифагора найдем СВ:

СВ² = АВ² - АС² = 36 - 9 = 27

СВ = √27 = 3√3 (см)

• Площадь прямоугольного треугольника равна половине произведения катетов.

$\displaystyle\bf S_{OCH}=\frac{1}{2}AC\cdot{CB}=\frac{1}{2}\cdot3\cdot3\sqrt{3}=\frac{9\sqrt{3} }{2} _{(CM^2)}$

2. Теперь надо найти высоту пирамиды.

SA = SB = SC (условие)

• Если все боковые ребра пирамиды равны, то вершина проецируется в центр описанной окружности основания.

Так как в основании лежит прямоугольный треугольник, то центр описанной окружности будет лежать на середине гипотенузы.

⇒ АН = НВ = 6 : 2 = 3 (см)

SH - высота пирамиды.

Рассмотрим ΔSCB = равнобедренный.

• Углы при основании равнобедренного треугольника равны.

⇒ ∠SBC = ∠SCB = 45°

• Сумма углов треугольника равна 180°.

⇒ ∠CSB = 90°

ΔSCB = равнобедренный, прямоугольный.

Пусть SC = SB = х см

Тогда по теореме Пифагора:

2х² = СВ²

$\displaystyle\bf x^2=\frac{27}{2}$

$\displaystyle\bf SB^2=\frac{27}{2}$

Рассмотрим ΔНSB - прямоугольный.

По теореме Пифагора найдем SH:

$\displaystyle\bf SH^2 = SB^2 - HB^2=\frac{27}{2}-9=\frac{9}{2} \\\\SH=\frac{3\sqrt{2} }{2} _{(CM)}$

3. Найдем объем пирамиды:

$\displaystyle\bf V(SABC)=\frac{1}{3}\cdot\frac{9\sqrt{3} }{2} \cdot\frac{3\sqrt{2} }{2}=\frac{9\sqrt{6} }{4}_{(CM^3)}$

Объем пирамиды равен $\displaystyle\bf \frac{9\sqrt{6} }{4}$  см³.

#SPJ1