Предмет: Алгебра, автор: rustamovarobiaaa0927

упростите выражение,

Приложения:

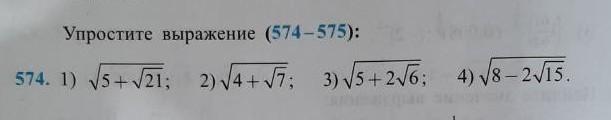
rustamovarobiaaa0927: а зачем нужно делить на 2?

GoldenVoice: Чтобы формула суммы или разности квадратов получалась с целыми числами. Возьмем первый пример. 5 должно раскладываться в сумму квадратов, а корень из 21 — в удвоенное произведение. Что же это за числа такие должны быть? Оказывается, корень из 3/2 и корень из 7/2. Как их подобрать?.. А так сделали типичное для математики действие — умножили и поделили числитель и знаменатель дроби на одно и то же число.

rustamovarobiaaa0927: хорошо спасибо большое

Ответы

Автор ответа: GoldenVoice

Ответ:

$1)\ \frac{{\sqrt {14} + \sqrt 6 }}{2};\ 2)\ \frac{{\sqrt {14} + \sqrt 2 }}{2};\ 3)\ \sqrt 3 + \sqrt 2 ;\ 4)\ \sqrt 5 - \sqrt 3$

Объяснение:

$1)\,\,\sqrt {5 + \sqrt {21} } = \sqrt {\displaystyle\frac{{10 + 2\sqrt {21} }}{2}} = \sqrt {\displaystyle\frac{{7 + 2\sqrt {21} + 3}}{2}} =\\\\= \sqrt {\displaystyle\frac{{{{(\sqrt 7 + \sqrt 3 )}^2}}}{2}} = \displaystyle\frac{{\sqrt 7 + \sqrt 3 }}{{\sqrt 2 }} = \displaystyle\frac{{\sqrt {14} + \sqrt 6 }}{2};$

$2)\,\,\sqrt {4 + \sqrt 7 } = \sqrt {\displaystyle\frac{{8 + 2\sqrt 7 }}{2}} = \sqrt {\displaystyle\frac{{7 + 2\sqrt 7 + 1}}{2}} =\\\\= \sqrt {\displaystyle\frac{{{{(\sqrt 7 + 1)}^2}}}{2}} = \displaystyle\frac{{\sqrt 7 + 1}}{{\sqrt 2 }} = \displaystyle\frac{{\sqrt {14} + \sqrt 2 }}{2};$

$3)\,\,\sqrt {5 + 2\sqrt 6 } = \sqrt {3 + 2\sqrt 6 + 2} = \sqrt {{{(\sqrt 3 + \sqrt 2 )}^2}} = \sqrt 3 + \sqrt 2 ;$

$4)\,\,\sqrt {8 - 2\sqrt {15} } = \sqrt {5 - 2\sqrt {15} + 3} = \sqrt {{{(\sqrt 5 - \sqrt 3 )}^2}} = \left| {\sqrt 5 - \sqrt 3 } \right| = \sqrt 5 - \sqrt 3 .$