Предмет: Геометрия,
автор: tursunmuratoshaxzod
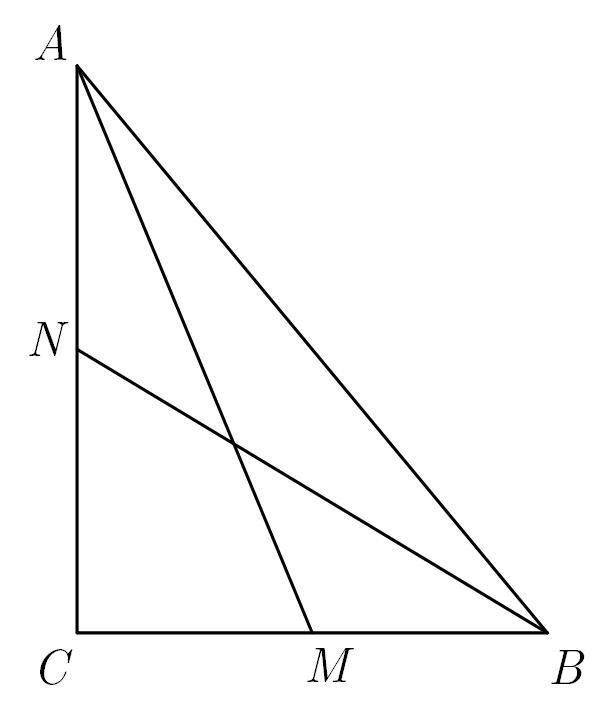
16. Медианы, проведенные к катетам прямоугольного треугольника, равны 15 и 6 под корнем 5. Найти гипотенузу треугольника.
Ответы
Автор ответа:
3
Ответ:
Гипотенуза треугольника равна 18
Объяснение:
Пусть ,
.
Тогда по теореме Пифагора из треугольника
а из треугольника
Получили систему уравнений
Из второго уравнения тогда
откуда
По теореме Пифагора из треугольника
Приложения:
cos20093:
Я только замечу :), не ставя под сомнение Ваше решение, что если есть система a² + (b/2)² = 15²; (a/2)² + b² = 5*6²; то можно просто сложить эти два уравнения (5/4)*(a² + b²) = 225+180 = 405; => c² = 81*4; c = 9*2 = 18;
Действительно правда! Спасибо!
Автор ответа:
4
Ответ:
18 ........................
Объяснение:
Приложения:


В первой строке небольшая печатная ошибка, появился корень из 6
Да , спасибо , но исправлять не буду . Кстати , если сложить квадраты этих медиан , то получится 5/4 (AB)^2 , что даёт ещё одно решение
5/4 (AB)^2 = 180 + 225
можно сказать , что это один из признаков прямоугольного треугольника
4ма^2 = 2(b^2 +c^2) -a^2 ; 4mb^2 = 2(a^2 +c^2) -b^2 ; 4ма^2 + 4mb^2 = 5c^2
пожалуй , самое короткое решение
демонстрирующее полезность формулы медианы
ма - медиана , проведённая из вершины А
добавил второе решение
Отлично!
Похожие вопросы
Предмет: Русский язык,
автор: ГАЙПРО
Предмет: Английский язык,
автор: Людок11
Предмет: Русский язык,
автор: LizaLizok020203
Предмет: Математика,
автор: ovana4661
Предмет: Английский язык,
автор: НикитаГневашев