Предмет: Алгебра,
автор: nastygor16
докажите равенство
Срочно 55 баллов
Приложения:
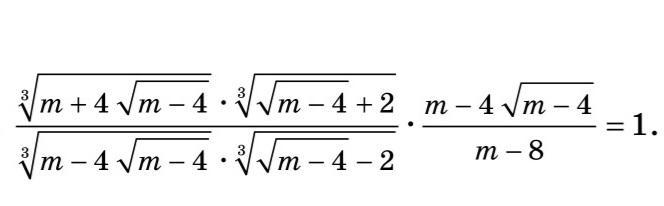
Ответы
Автор ответа:
1
Объяснение:
Выражение под первым корнем в числителе:
Так как
то
Аналогично в знаменателе
Тогда значение выражения слева с помощью формулы разности квадратов:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: balkonstroi2002
Предмет: Другие предметы,
автор: Alina4564
Предмет: Қазақ тiлi,
автор: АринаБогданова
Предмет: Английский язык,
автор: Anastasia200600
Предмет: Математика,
автор: lalkanik