Question

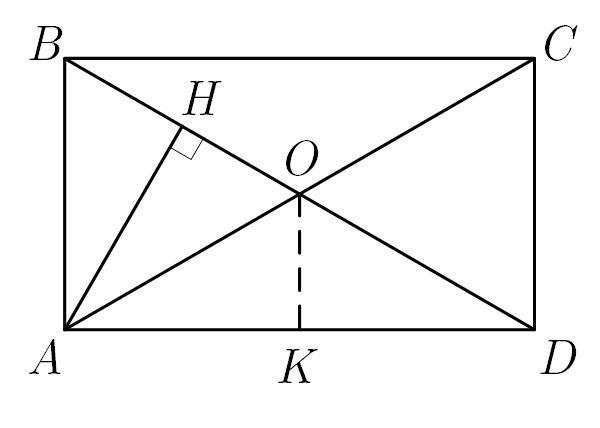
перпендикуляр опущений з вершини A прямокутника ABCD на діагональ, ділить її у відношенні 1:3 рахуючи від вершини B. Знайдіть відстань від точки перетину діагоналей прямокутника до його більшої сторони, якщо довжина діагоналі 6 см

Answer 1

Ответ:

1,5

Объяснение:

Пусть $BH = x$, $HD = 3x$. По условию $x + 3x = 6,\ x = 1{,}5.$

Тогда высота $AH = \sqrt {BH \cdot HD} = \sqrt {x \cdot 3x} = x\sqrt 3 = 1{,}5\sqrt 3 .$

Из прямоугольного треугольника $AHB$

$AB = \sqrt {B{H^2} + A{H^2}} = \sqrt {{x^2} + {{(x\sqrt 3 )}^2}} = 2x = 3.$

Искомый отрезок $OK$ — средняя линия треугольника $BDA$, $OK = \displaystyle\frac{1}{2}BA = \displaystyle\frac{3}{2} = 1{,}5.$

Answer 2

Відповідь: 1,5 см.

АН перпендикуляр, проведений с прямого кута до гіпотенузи. ВН=6÷(1+3)=1,5 см. За метричним співвідношенням сторін АВ^2=ВН×АС=1,5×6=9, тоді АВ=3 см. ОК-відстань від точки перетину діагоналей до більшої сторони, яка є середньою лінією трикутника АВD . ОК=АВ:2=3:2=1,5 см.