Question

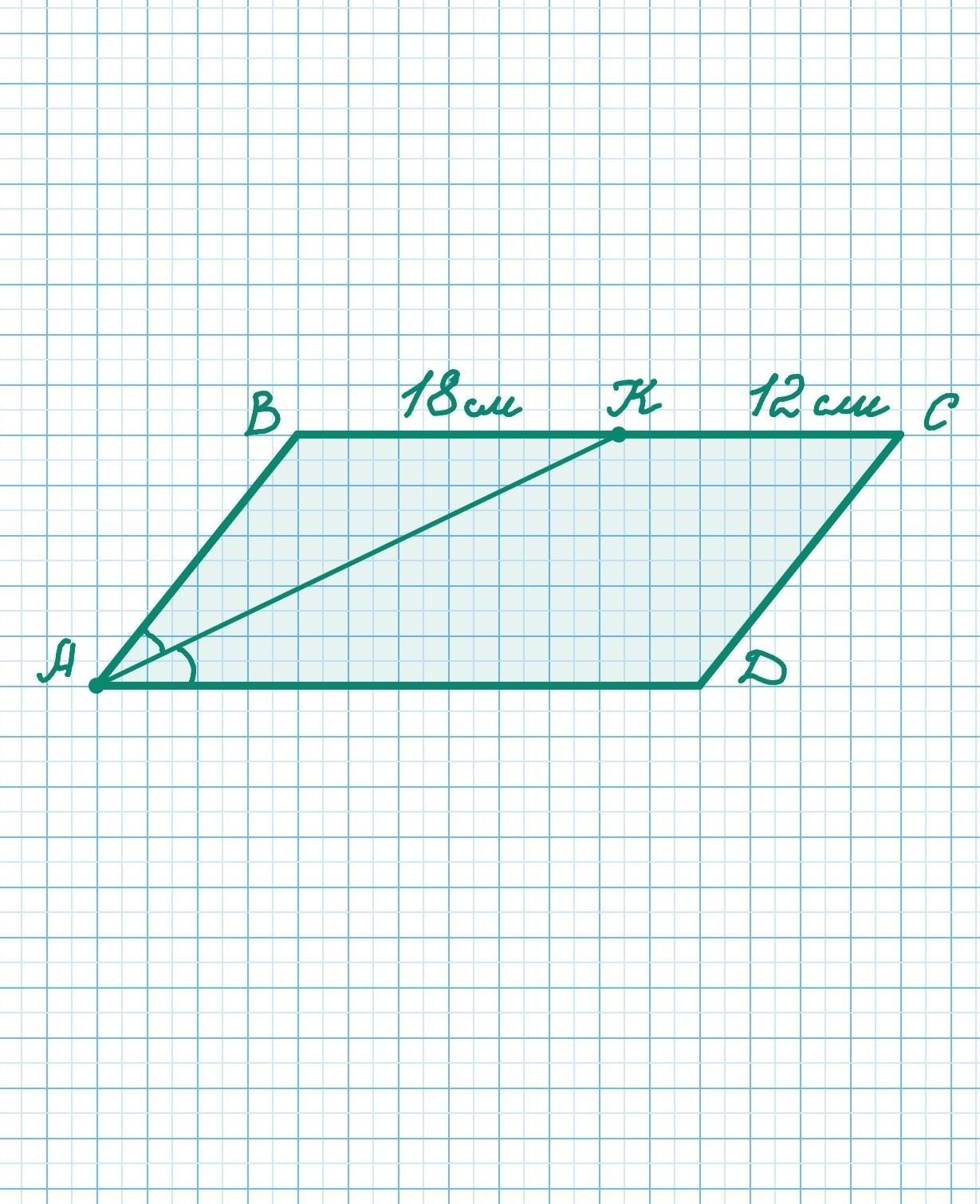
Кут А паралелограма ABCD дорівнює 30°. Бісектриса кута А перетинає пряму ВС у точці К такій, що ВК-18 см, СК = 12 см. Знайдіть площу паралелограма ABCD.​

Answer 1

Ответ:

Площадь параллелограмма равна 270 см²

Объяснение:

Угол А параллелограмма АВСD равен 30°. Биссектриса угла А пересекает прямую ВС в точке К так, что ВК=18 см, СК=12 см. Найдите площадь параллелограмма ABCD.

• Параллелограмм - это четырёхугольник, у которого противоположные стороны попарно параллельны и равны.

Так как АК - биссектриса ∠А, то ∠ВАК=∠DAK -по свойству биссектрисы.

∠DAK=∠AKB - как внутренние накрест лежащие углы при параллельных прямых BC и AD и секущей AK.

Следовательно ∠BAK=∠AKB, а △АВК - равнобедренный, так как углы при основании AK равны.

• В равнобедренном треугольнике боковые стороны равны.

Следовательно АВ=ВК=18см

AD=ВС=ВК+КС=18+12=30 см.

• Площадь параллелограмма равна произведению соседних сторон на синус угла между ними:

S=a•b•sinα

S(ABCD) = AB•AD•sin30°=18•30•½= 9•30= 270 см²