Предмет: Геометрия,
автор: agentgames1
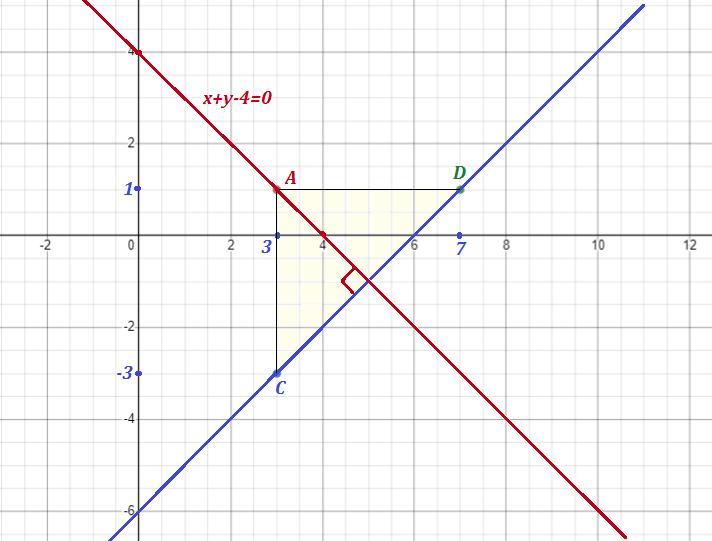
Напишите уравнение прямой, проходящей через точку A[3;1], перпендикулярную прямой проходящей через точки C[3;-3] и D[7;1]. Тогда площадь треугольника этого
прямая линия создает с осями координат
Ответы
Автор ответа:
1
Ответ:
Через точку А(3;1) проходит прямая , перпендикулярная прямой CD ,
С(3;-3) , D(7;1) .
Вектор . Вектор CD будет перпендикулярен прямой
.
Уравнение прямой , проходящей через точку А , перпендикулярно CD имеет вид
Площадь треугольника АСD равна полупроизведению катетов, так как треугольник получился прямоугольный .
Длины катетов равны AD=7-3=4 , AC=1-(-3)=4 .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: nbandit
Предмет: Английский язык,
автор: martyn9333
Предмет: Русский язык,
автор: DuseevaAlino4ka
Предмет: Математика,
автор: cleyns
Предмет: Английский язык,
автор: Аноним