Предмет: Математика,
автор: miishakryt
найти производную кроме первого номера
Приложения:
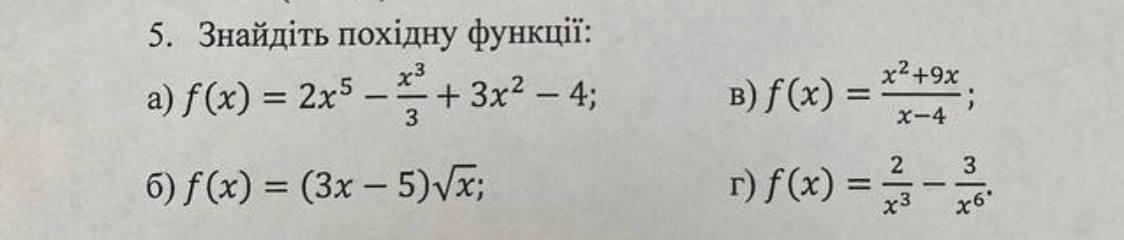
Ответы
Автор ответа:
0
Ответ:
б)
в)
г)
Пошаговое объяснение:
Найти производную функций:
б)
Производная произведения:
Производная степенной функции:
в)
Производная частного:
г)
Похожие вопросы
Предмет: Русский язык,
автор: medvedus2000
Предмет: Окружающий мир,
автор: Энджело
Предмет: Английский язык,
автор: 555otlichnik5555
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: lyubavlasova10