Question

ОЧЕНЬ НУЖНО, СДЕЛАЙТЕ ПОЖАЛУЙСТА!!! а, б, в

Answer 1

Пошаговое объяснение:

Выполним преобразование уравнения:

$y = 2{x^2} + 8x + 2 = 2({x^2} + 4x + 1) = 2({x^2} + 4x + 4 - 3) =\\\\= 2({x^2} + 4x + 4) - 6 = 2{(x + 2)^2} - 6.$

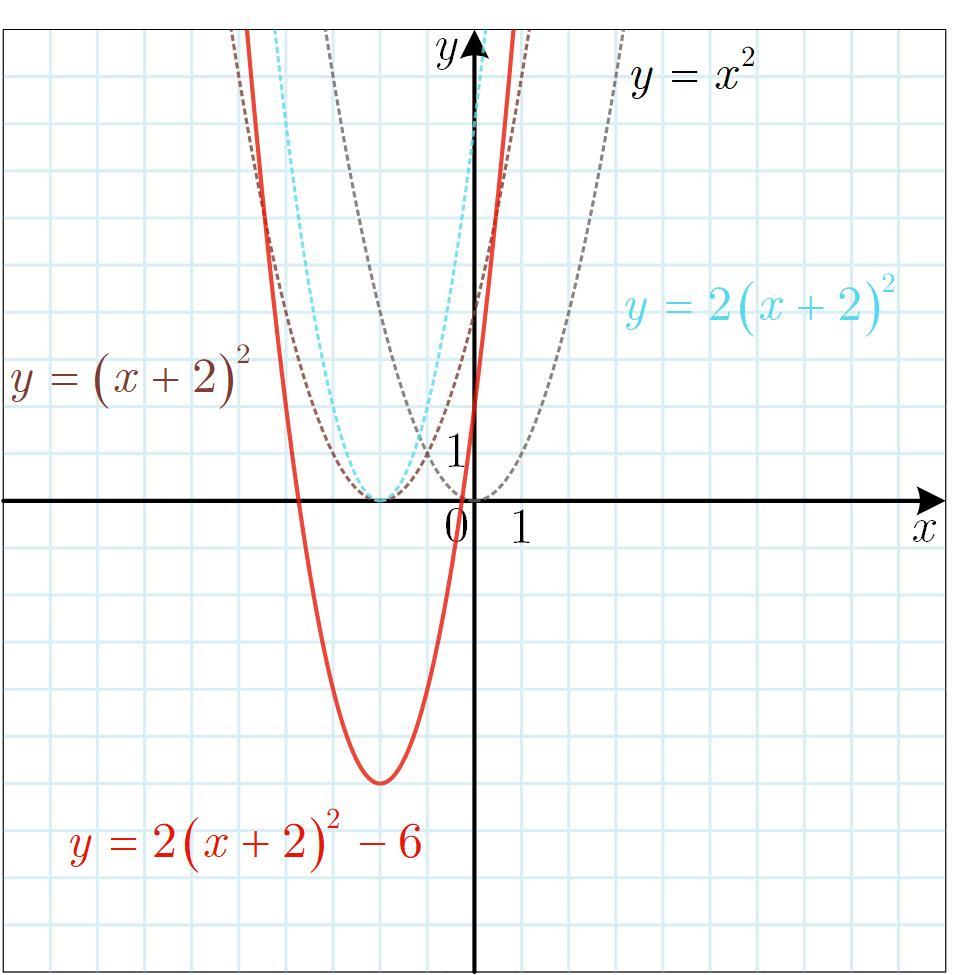
Теперь понятно, что график данной функции можно получить по такой схеме (см. рис. 1):

$y = {x^2}\,\, \to \,\,y = {(x + 2)^2}\,\, \to \,\,y = 2{(x + 2)^2}\,\, \to \,\,y = 2{(x + 2)^2} - 6$

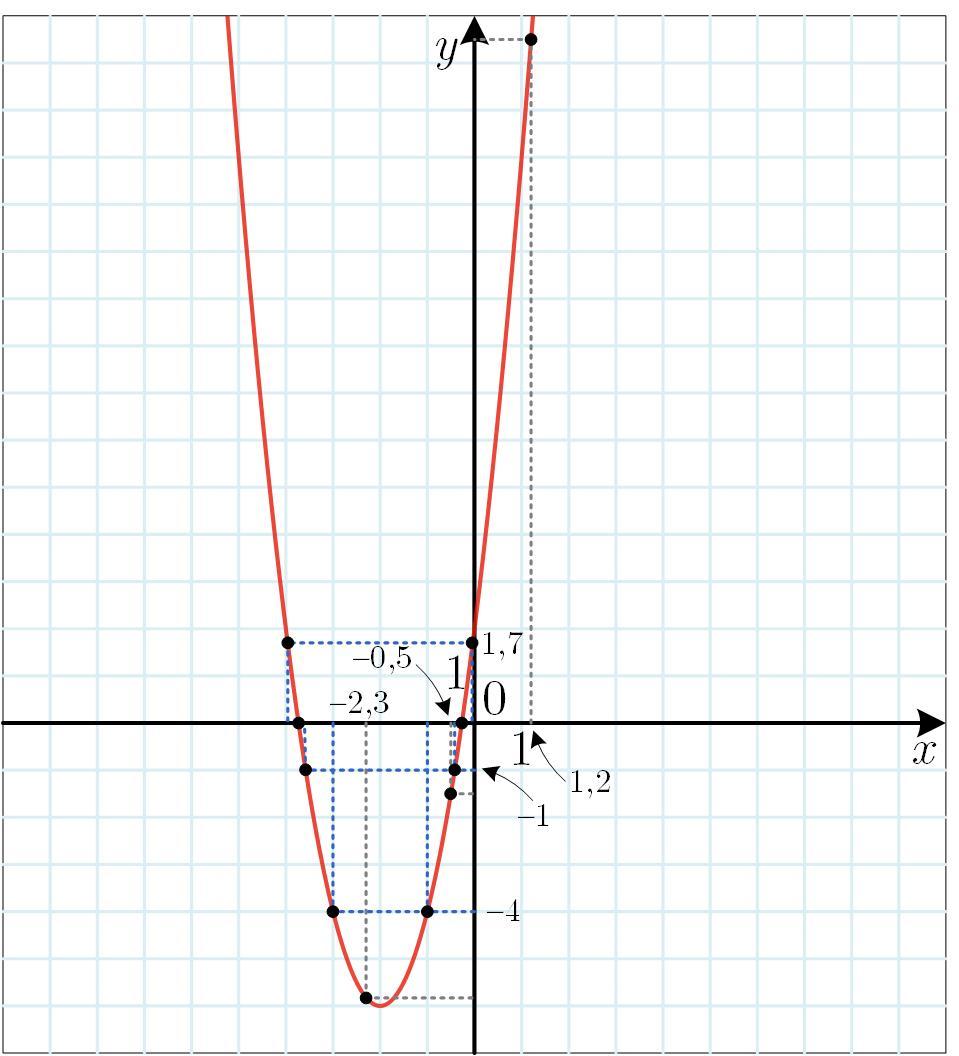
а) Отметим на оси $x$ точки, соответствующие числам –2,3; –0,5; 1,2. Через эти точки проведем вертикальные прямые до пересечения с графиком функции, после чего определим координату этой точки по оси $y.$ Графический метод дает очень приближенный результат и сильно зависит от точности и детальности рисунка.

По рисунку видно, что

при $x = - 2{,}3$ $y \approx - 5{,}8;$

при $x = - 0{,}5\ y \approx - 1{,}5;$

при $x = 1{,}2\ y \approx 14{,}5.$

б) Аналогично, на оси y отметим точки, соответствующие числам  –4;  –1; 1,7.

По рисунку видно, что

при $y = - 4\ x = - 3$ и $x = - 1;$

при $y = - 1\ x \approx - 3{,}6$ и $x \approx - 0{,}4;$

при $y = 1{,}7$ $x \approx - 4$ и $x \approx 0.$

в) Нули функции — точки, в которых значение функции равно 0, т. е. точки пересечения графика с осью $x$. По рисунку видно, что $x \approx - 3{,}7$ и $x \approx - 0{,}3.$

$y > 0$ левее левой точки и правее правой, т. е. при

$x \in ( - \infty ;\,\, - 3{,}7) \cup ( - 0{,}3;\,\, + \infty ).$

$y < 0$ между найденными точками, т. е. при

$x \in ( - 3{,}7;\,\, - 0{,}3).$

г) Парабола расположена ветками вверх, поэтому функция убывает на ее левой ветке, а возрастает — на правой. Ветки сходятся в вершине параболы, ее координата ${x_B} = - 2.$

Следовательно, функция убывает при $x \in ( - \infty ;\,\, - 2]$ и возрастает при $x \in [ - 2;\,\, + \infty ).$

#SPJ1