Предмет: Математика,
автор: denizka76
Срочно пж. Математика
Приложения:
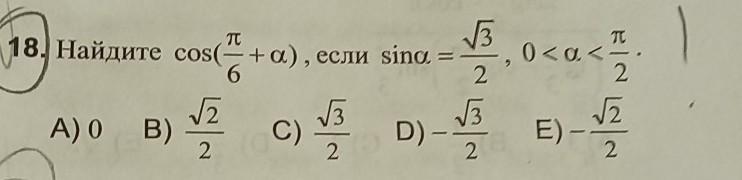
bertramjeratire:
А) 0
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
sin a = √3/2
Похожие вопросы
Предмет: Русский язык,
автор: Kalganova1984
Предмет: Қазақ тiлi,
автор: KotoCrew
Предмет: Окружающий мир,
автор: настяПермякова2006
Предмет: Английский язык,
автор: Assassinl
Предмет: Английский язык,
автор: AnastasuaFill