ребята пожалуйста что знаете. Буду максимально благодарен!
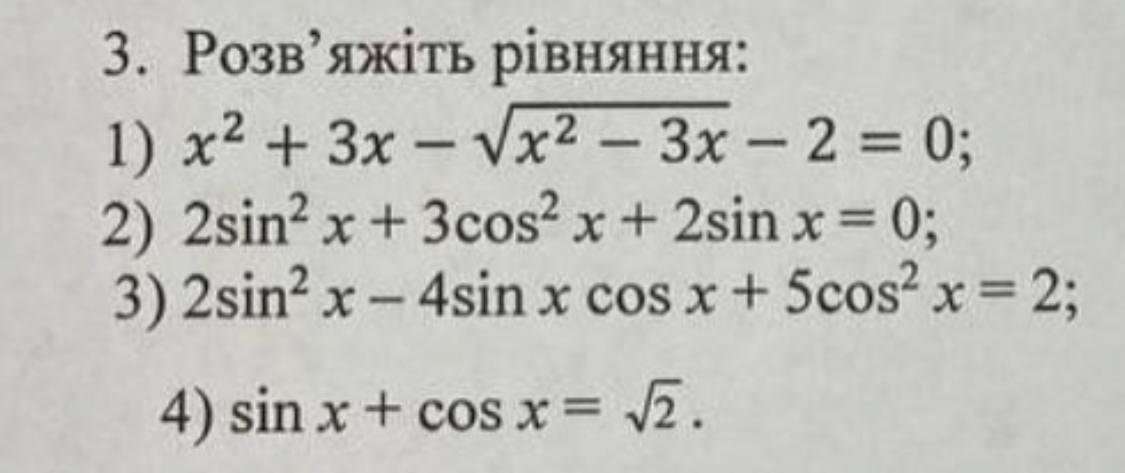
Ответы
Ответ:
1) ошибка в условии;
Пошаговое объяснение:
1) Вероятно, в задании опечатка и следует считать, что под корнем стоит , иначе уравнение имеет единственный корень, приблизительно равный
Тогда делая замену получаем квадратное уравнение
По теореме Виета
откуда
Подставляя найденное значение обратно, получаем
2) Применим универсальное тригонометрическое тождество
Сделаем замену
Второй корень в силу того, что посторонний.
Значит
3) Воспользуемся универсальным тригонометрическим тождеством
Решение первого уравнения —
Для решения второго уравнения вначале убедимся, что не является его решением (если это так, то по основному тригонометрическому тождеству
и левая часть не может превращаться в 0). Тогда на
можно разделить обе части:
4)
Разделим обе части уравнения на :
Коэффициенты возле синуса и косинуса — такие числа, сумма квадратов которых равна 1. Значит они могут быть синусом и косинусом какого-то угла (например,
).
Тогда с учетом применения формулы синуса суммы
получаем