Предмет: Геометрия, автор: liftec74

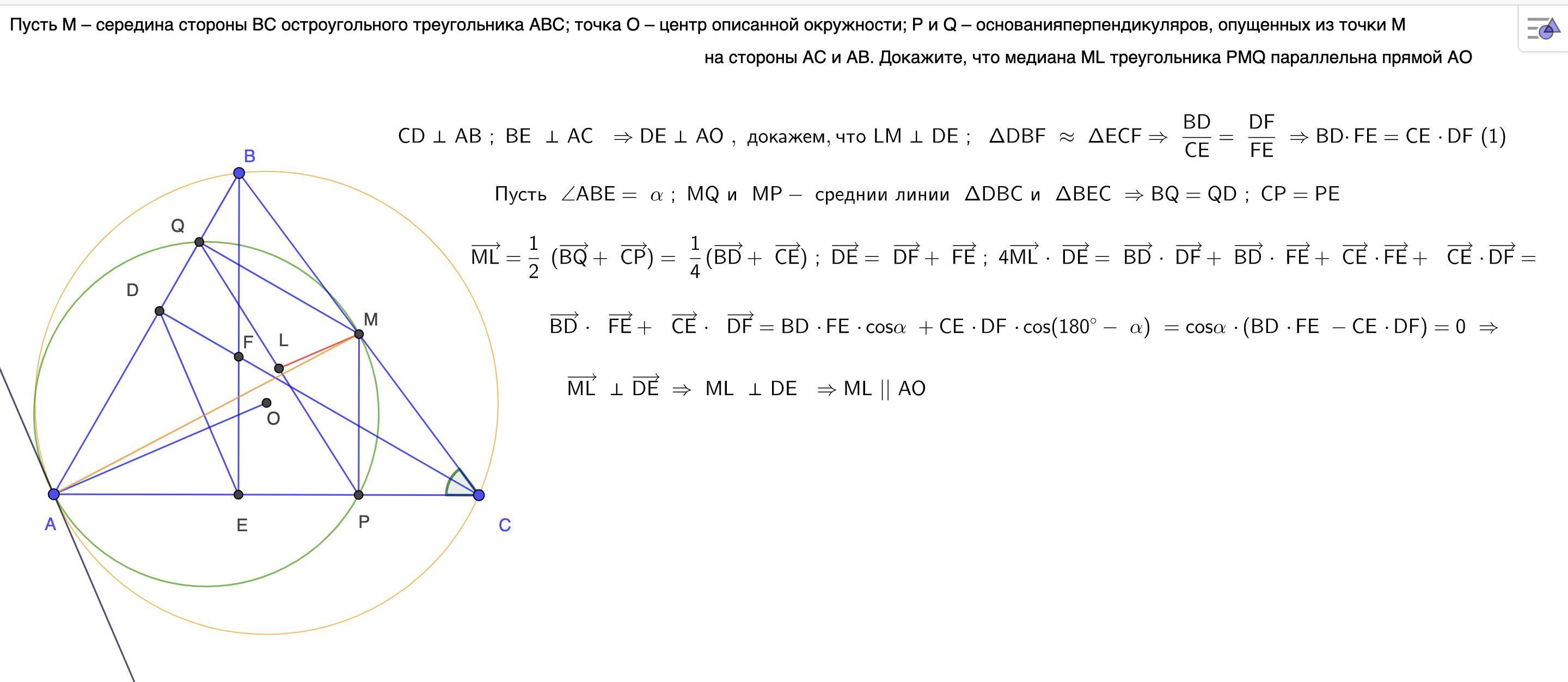
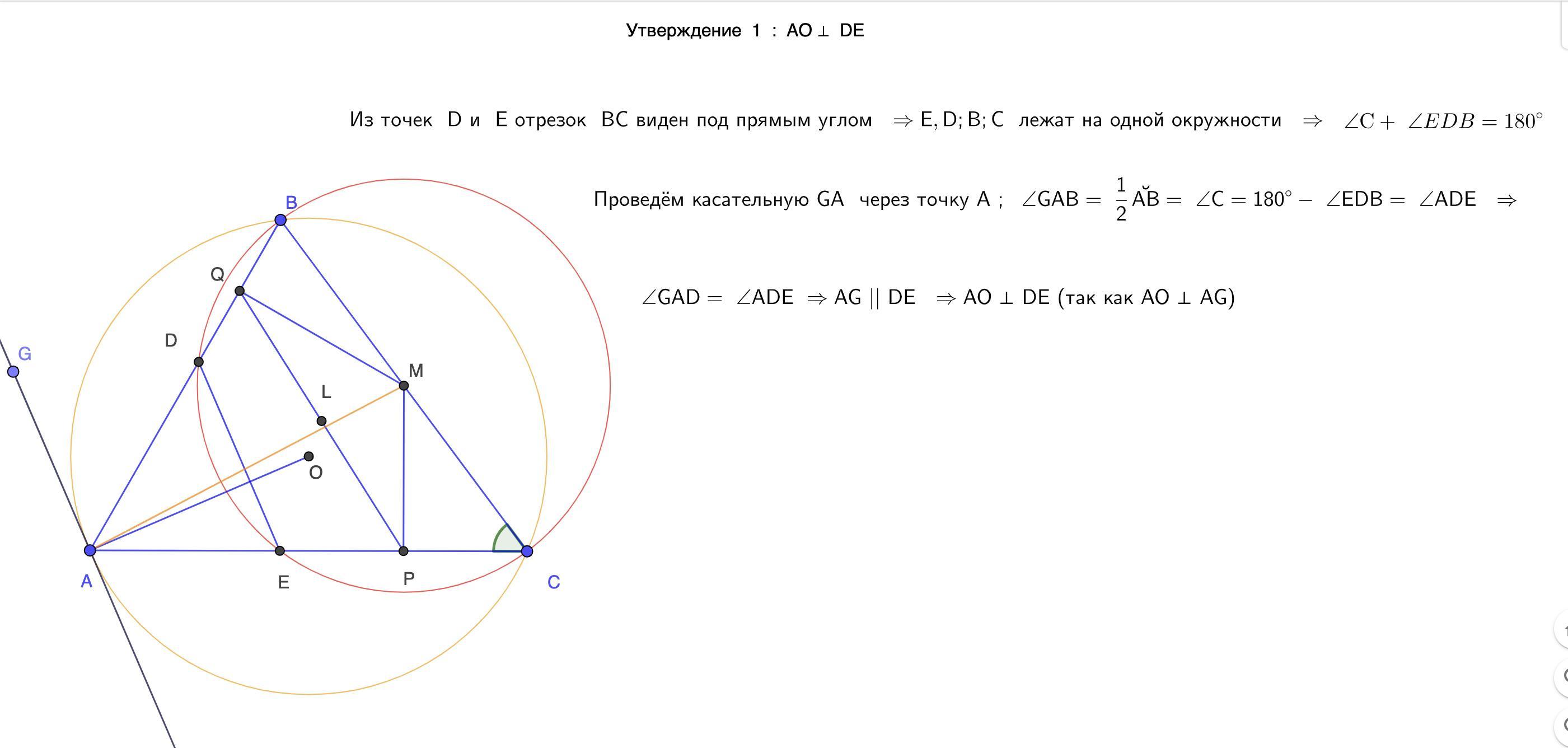
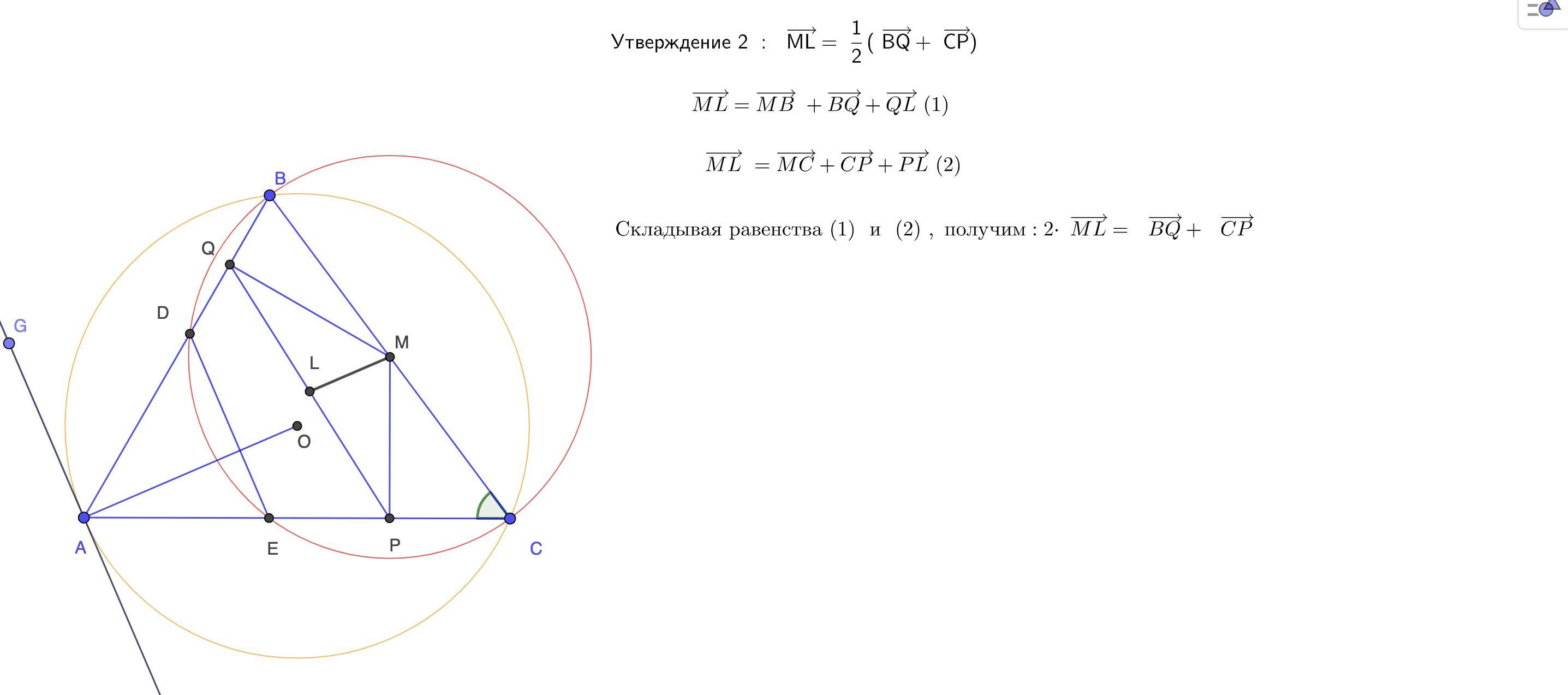
Пусть M – середина стороны BC остроугольного треугольника ABC; точка O – центр описанной окружности; P и Q – основания
перпендикуляров, опущенных из точки M на стороны AC и AB. Докажите, что медиана ML треугольника PMQ параллельна прямой AO

liftec74: OK. Спасибо за идею. Но все таки хотелось бы решить так, как было задумано автором. Стр 47 журнала.

antonovm: вообщем векторное решение у меня уже есть , пробую найти классическое

antonovm: коротенькое решение получилось , так как 2 утверждения применил без доказательства , одно из свойств ортотреугольника , а второе из векторной алгебры

antonovm: доказательство этих утверждений приведу отдельно ( если успею )

liftec74: В Вашем решении полностью разобрался. Так что добавлять что-либо нет необходимости. Если все-таки возникнут мысли как решить задачу , используя подобие и свойство медиан в подобных треугольниках, то дайте знать пожалуйста. Еще раз спасибо за прекрасное решение.

siestarjoki: хорошая задача, тоже решу

siestarjoki: i.imgur.com/PYDq3H2.png

antonovm: Класс !

antonovm: Спасибо

liftec74: Спасибо. Тоже замечательное решение.