Предмет: Алгебра,
автор: brainly2949
Завдання на фото ....
Приложения:
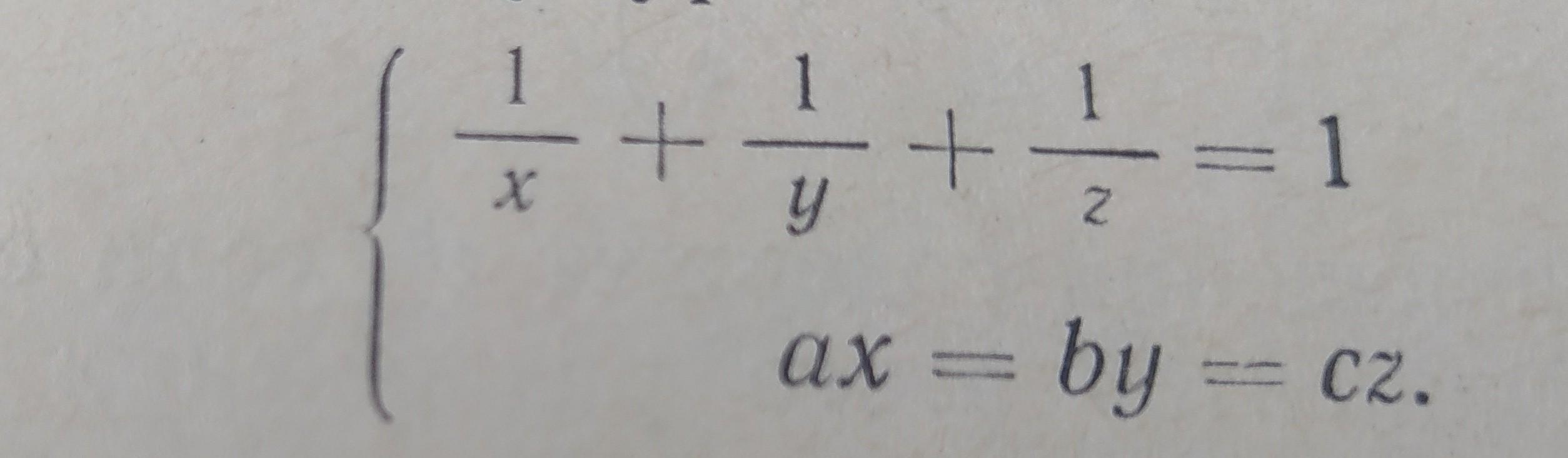
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Подразумеваем, что коэффициенты не равны 0.
Тогда
Подставим эти значения в первое уравнение:
Тогда
Автор ответа:
1
Ответ: .
, a, b, c - коэффициенты, отличные от 0 .
Выразим две переменные через третью переменную. Например, переменные х и у через z . Для этого используем второе уравнение
Подставим всё в первое уравнение.
Похожие вопросы
Предмет: Русский язык,
автор: SApevalova
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: dumnovd
Предмет: Русский язык,
автор: forzit
Предмет: Литература,
автор: Аноним