Question

У коло радіуса R вписано трапецію, нижня основа якої вдвічі більша від
кожної з решти сторін. Знайти площу трапеції.​

Answer 1

Ответ:

В окружность радиуса R вписана трапеция, нижнее основание которой вдвое больше каждой из остальных сторон . Найти площадь трапеции.

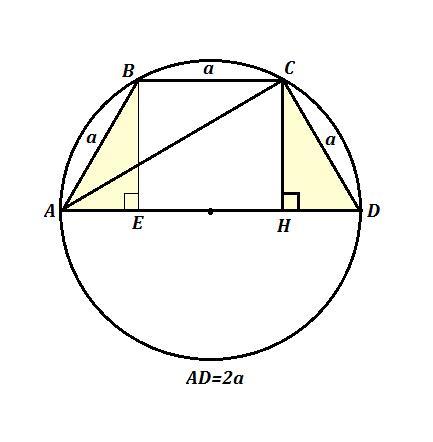
     Так как в окружность можно вписать только равнобедренную трапецию, то АBCD - равнобедренная трапеция , АВ=CD .

Причём по условию, если нижнее основание обозначить  2а , то  боковые стороны и верхнее основание равны  а=АВ=BC=CD .

  Опустим перпендикуляры  ВЕ и СН на AD . Получим прямоугольник ВСНЕ ( ВС=НЕ  и ВЕ=СН ) , тогда НЕ=ВС=а  и  ΔАВЕ=ΔCDH по гипотенузе (АВ=CD=а) и катету (ВЕ=CН)   ⇒  

HD=AE=(AD-HE):2=(2a-a):2=a/2

Из ΔCDH по теореме Пифагора найдём катет СН, который является высотой трапеции :

$CD^2=CH^2+HD^2\ \ ,\ \ CH=\sqrt{CD^2-HD^2}=\sqrt{a^2-\dfrac{a^2}{4}}=\sqrt{\dfrac{3a^2}{4}}=\bf \dfrac{a\sqrt3}{2}$

Рассмотрим ΔАСН.

 $AH=AD-HD=2a-\dfrac{a}{2}=\bf \dfrac{3a}{2}$    .

По теореме Пифагора:  

$AC^2=AH^2+CH^2=\dfrac{9a^2}{4}+\dfrac{3a^2}{4}=\dfrac{12a^2}{4}=3a^2\ ,\ \ \bf AC=a\sqrt3$

Рассмотрим ΔACD . Окружность , описанная около заданной трапеции является одновременно и окружностью, описанной около  ΔACD . Известна формула площади треугольника, выраженная через радиус описанной окружности:  $\bf S=\dfrac{abc}{4R}$  .  Поэтому имеем:

$S_{ACD}=\dfrac{AD\cdot CD\cdot AC}{4R}=\dfrac{2a\cdot a\cdot a\sqrt3}{4R}=\bf \dfrac{a^3\sqrt3}{2R}$  

Можно выразить площадь ΔACD через высоту:

$S_{ACD}=\dfrac{1}{2}\cdot AD\cdot CH=\dfrac{1}{2}\cdot 2a\cdot \dfrac{a\sqrt3}{2}=\bf \dfrac{a^2\sqrt3}{2}$  

Приравняем площади и найдём a .

$\dfrac{a^3\sqrt3}{2R}=\dfrac{a^2\sqrt3}{2}\ \Big|:\dfrac{a^2\sqrt3}{2}\ \ \ \ \ \ \Rightarrow \ \ \ \dfrac{a}{R}=1\ \ \ \Rightarrow \ \ \ \bf a=R$  

Тогда можно записать, что

 $\bf AB=BC=CD=R\ ,\ \ \ AD=2R\ ,\ \ \ \ CH=\dfrac{R\sqrt3}{2}$  .

Площадь трапеции равна  

$S=\dfrac{AD+BC}{2}\cdot CH=\dfrac{2R+R}{2}\cdot \dfrac{R\sqrt3}{2}=\dfrac{3R\cdot R\sqrt3}{2\cdot 2}=\dfrac{3\sqrt3\cdot R^2}{4}$  

Ответ:   $\bf S=\dfrac{3\sqrt3\cdot R^2}{4}$  .

 Замечание .  Так как получили, что АВ=ВС=CD=R  и  AD=2R , то центр описанной окружности лежит посередине бОльшего основания трапеции, то есть основание AD является диаметром описанной окружности . И треугольники АОВ , ВОС и COD являются правильными, а углы при основаниях этой трапеции равны по 60° и 120° .