Предмет: Геометрия,
автор: aartdesignerr
Геометрия 20 БАЛЛОВ!
Приложения:
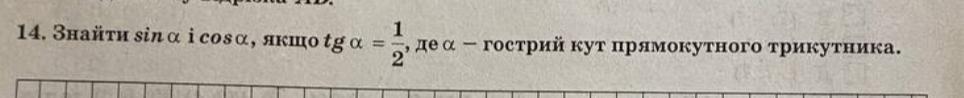
Ответы
Автор ответа:
2
Ответ:
Объяснение:
1 способ.
Применим тригонометрическую формулу:
Учитывая, что
, получаем:
2 способ.
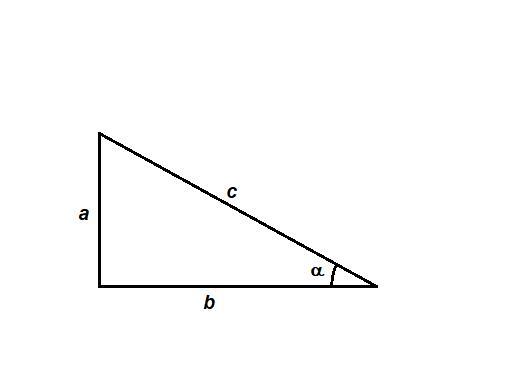
- Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему:
Пусть х - длина стороны а, тогда 2х - длина стороны b.
По теореме Пифагора:
- Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе:
- Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе:
Приложения:
Автор ответа:
1
Розв'язання завдання додаю.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: gacenbiler0302
Предмет: Английский язык,
автор: HappiAngel
Предмет: Русский язык,
автор: ebakopat
Предмет: Математика,
автор: masuma18
Предмет: Математика,
автор: Аноним