Question

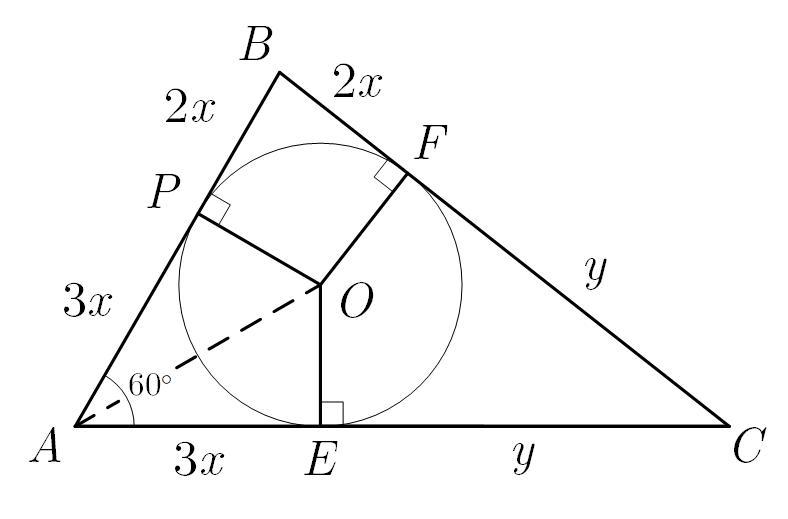
В треугольник ABC вписана окружность, касающаяся сторон AB, BC и AC в точках P,F и Е соответственно. Найдите отношение FÇ к FB, если AP относится к PB как 3:2. Угол BAC=60°​

Answer 1

Ответ:

$FC:FB = 5:2$

Пошаговое объяснение:

Пусть $AP = 3x$, а $PB = 2x$.

Учитывая тот факт, что отрезки касательных, проведенные к окружности из одной точки, равны, $BF = PB = 2x$, $AE = AP = 3x$. Пусть $CF = CE = y.$

Полупериметр треугольника $ABC$

$p = \displaystyle\frac{{(3x + 2x) + (2x + y) + (3x + y)}}{2} = 5x + y,$

а его площадь по формуле Герона

$S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {(5x + y) \cdot 3x \cdot 2x \cdot y} = x\sqrt {6y(5x + y)} .$

Так как центр окружности, вписанной в треугольник, — точка пересечения биссектрис, то $AO$ разбивает угол $A$ на два угла по $30^\circ$  каждый. Тогда из прямоугольного треугольника $AEO$

$OE = r = 3x{\mathop{\rm tg}\nolimits} 30^\circ = 3x \cdot \displaystyle\frac{{\sqrt 3 }}{3} = x\sqrt 3 .$

Но радиус вписанной в треугольник окружности вычисляется по формуле

$r = \displaystyle\frac{S}{p},$

поэтому

$x\sqrt 3 = \displaystyle\frac{{x\sqrt {6y(5x + y)} }}{{5x + y}};\\\\\sqrt {5x + y} = \sqrt {2y} ;\\\\5x + y = 2y;\\\\y = 5x.$

Значит $FC:FB = y:2x = 5x:2x = 5:2.$

Answer 2

Ответ:

5 : 2  ....................................

Пошаговое объяснение: