Предмет: Геометрия,
автор: Shush0509
Пожалуйста,решите.Очень срочно!!!
Приложения:

MCFoger:
площа чого дорівнює 204?
Ответы
Автор ответа:
2
Ответ:
либо
Объяснение:
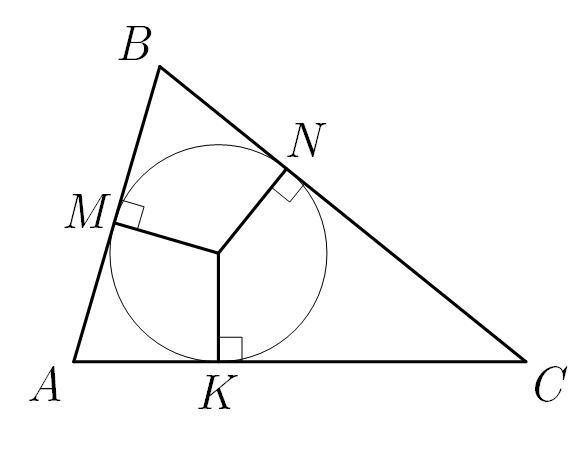
Пусть . Тогда
как отрезок касательной к окружности, проведенной из одной точки. По условию
. Пусть точка касания
разбивает отрезок
на два длиной
и
. Тогда
Стороны треугольника ,
,
. Периметр треугольника
По формуле Герона площадь треугольника равна
а радиус вписанной окружности
Из последнего равенства получаем, что .
Тогда из равенства для площади
Несмотря на два ответа, речь идет об одном и том же треугольнике со сторонами 17 см, 25 см и 26 см, где сторона , а стороны
и
могут принимать значения соответственно 25 см и 26 см или 26 см и 25 см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Bysa25051
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: vlad1234078
Предмет: Биология,
автор: sv9toi92