Предмет: Алгебра,
автор: iliakuruch9
Помогите решить уравнение, применив подстановку
Приложения:
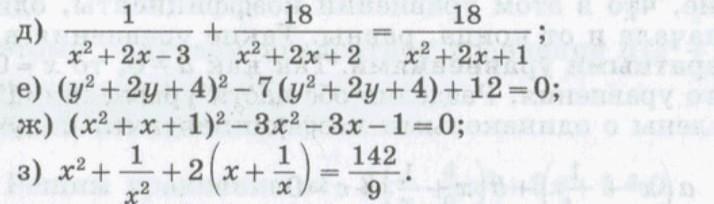
Cohendd:
Не подстановку, а замену переменной. Больше трёх нельзя.
Замена переменной — школьный термин, в высшей математике это называется именно словом "подстановка" (семантическая калька фр. substitution)
Ответы
Автор ответа:
2
Подстановка
ОДЗ: t != 4, t != -1, t!=0
Первый случай:
Второй случай:
Ответ:
==========
Подстановка
Первый случай:
Второй случай:
Ответ:
=====
Подстановка
Корни легко подбираются по теореме Виета:
Первый случай:
Второй случай:
Ответ:
=========
Это так называемое возвратное уравнение. Пусть выражение в скобках равно . Если возвести его в квадрат, получим:
Откуда
Первый случай:
Второй случай:
Ответ:
Да. Если я в детстве спрашивала, как пишется слово, мне отвечали и добавляли: падежОв не знаешь. Я первый раз спросила, почему так. Это же неверно. Мне объяснили, что каждый многого не знает и ошибка именно об этом.
У нас Школьные знания, а не Вышка. Прочтите свой комментарий. Калька, французский.... Гений.... А задание школьное) Так чего заноситься?
А ничего, что вы первая исправили человека? Не я пришёл в комментарии под вашим заданием со словосочетанием «замена переменной» и сказал, что нужно написать «подстановка». Я вам не грубил, а обоснованно ответил, почему слово «подстановка» в данном контексте точно не является ошибкой (а в старых советских школьных задачниках именно оно и использовалось).
Ваши претензии напоминают мне «предъявы» двоечников «ты шо, самый умный тут?» Очень странно видеть такую позицию от учительницы.
Никнейм я придумал ещё лет 6 назад, не вкладывая в него глубокого смысла, а отсылка на французский была не потому, что это «элитарный язык», а потому что данное слово ввели французские математики, которые формализовывали мат. анализ в 19 веке, такие как Коши. Как и многие другие слова современной мат. терминологии.
Ещё и Украину приплели, мда. Хотя сейчас это неудивительно. Подозреваю, что это главная причина, почему вы возмутились.
Нет. Ошибаетесь. Сейчас многие украинцы размахивают флагом. И комментарий написала не Вам, а автору вопроса. А я как была советской, так и доживу. Про деликатность не забывайте. Хорошая вещь)))
Ответить по существу нечего, поэтому продолжаем об Украине, я понял.
А что для Вас существо? На что я должна ответить? У нас с Вами разные взгляды. А в физике я тоже могу сыпать терминами. Только зачем? Я дольше на сайте, чем Вы. Работаю каждый день. 3 грамоты за модераторство + тыщ 17-18 грамотно решённых задач. Видела всякое. Модерам достается. Желаю здравствовать!))
Вы большой молодец, отличный учитель, только зачем мне об этом пишете?:) Я вашу квалификацию не оспаривал. И вам всего доброго.
Похожие вопросы
Предмет: Русский язык,
автор: саша3125
Предмет: Русский язык,
автор: likauvanova140
Предмет: Русский язык,
автор: Zed2234
Предмет: Математика,
автор: dutkabun