Question

Помогите пожалуйста Срочно 12 и 17 я вас прошу с объяснением ПОЖАЛУЙСТА
Даю 26 балов

Answer 1

Ответ:

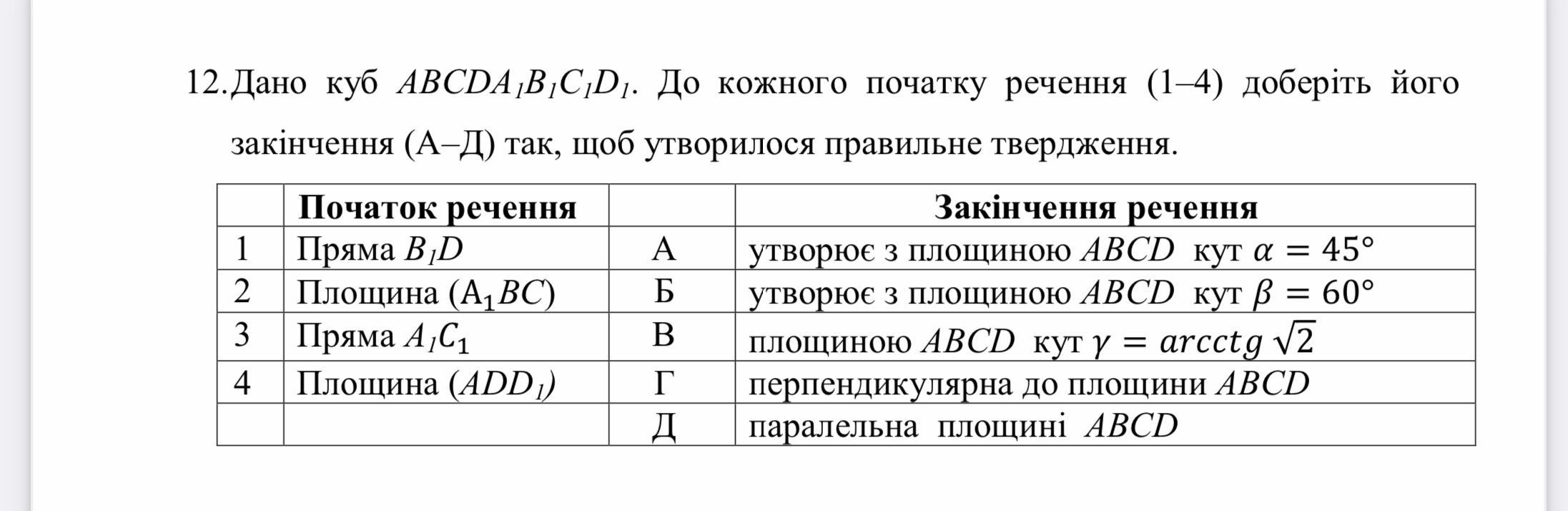
12. 1В, 2А, 3Д. 4Г;

17. 33,49

Пошаговое объяснение:

12

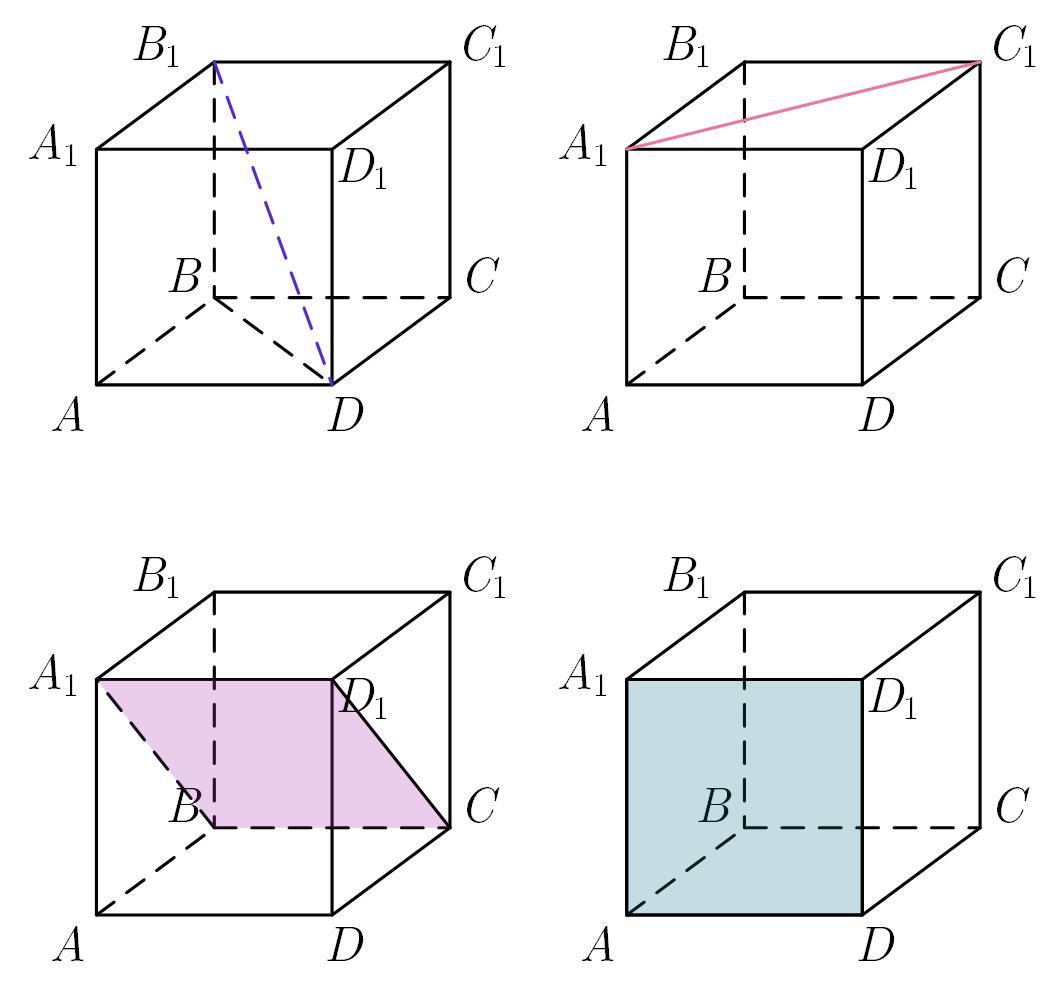
Во всех приведенных задачах речь идет о взаимном расположении элементов (прямых, плоскостей) и одной из граней куба.

1—В

Поскольку ортогональной проекцией отрезка ${B_1}D$ на плоскость $ABCD$ является отрезок $BD$, то угол, который образуют прямая с плоскостью — угол между прямыми ${B_1}D$ и $BD$, т. е. $\angle {B_1}DB.$

Пусть ребро куба равно $a$. Тогда диагональ квадрата $BD$ можно найти по теореме Пифагора из треугольника $ABD$: $BD = \sqrt {{a^2} + {a^2}} = a\sqrt 2 .$ Тогда по теореме Пифагора из треугольника ${B_1}BD$

${B_1}D = \sqrt {{a^2} + {{(a\sqrt 2 )}^2}} = \sqrt {3{a^2}} = a\sqrt 3 .$

Из прямоугольного треугольника ${B_1}BD$

${\mathop{\rm ctg}\nolimits} \angle {B_1}DB = \displaystyle\frac{{BD}}{{B{B_1}}} = \displaystyle\frac{{a\sqrt 2 }}{a} = \sqrt 2 ,$

откуда $\angle {B_1}DB = {\mathop{\rm arcctg}\nolimits} \sqrt 2 .$

2—А

Построим сечение куба плоскостью ${A_1}BC$. Точки ${A_1} - B$ и $B - C$ можно соединить, так как каждая из этих пар лежит в одной плоскости. Линии пересечения двух параллельных плоскостей третьей параллельны, поэтому из точки $C$ проводим линию параллельно $B{A_1}.$

Плоскости $ABCD$ и $B{A_1}{D_1}C$ образуют двугранный угол, величина которого равна величине угла ${D_1}CD$. Это угол, который образует диагональ квадрата с его стороной, он равен $45^\circ .$

3—Д

Так как прямая ${A_1}{C_1}$ параллельна прямой $AC$ в плоскости $ABCD$, то по признаку параллельности прямой и плоскости они параллельны.

4—Г

В кубе смежные грани перпендикулярны друг другу.

17

Пусть радиус основания цилиндра равен $r$. Тогда треугольник $AOD$ равнобедренный с углом $120^\circ$ при вершине, значит углы при основании равны

$\displaystyle\frac{{180^\circ - 120^\circ }}{2} = 30^\circ .$

По теореме синусов

$\displaystyle\frac{{AO}}{{\sin 30^\circ }} = \displaystyle\frac{{AD}}{{\sin 120^\circ }};\\\\AD = \displaystyle\frac{{AO\sin 120^\circ }}{{\sin 30^\circ }};\\\\AD = \displaystyle\frac{{r \cdot \displaystyle\frac{{\sqrt 3 }}{2}}}{{\displaystyle\frac{1}{2}}} = r\sqrt 3 .$

В прямоугольном треугольнике $BAD$

$BA = AD{\mathop{\rm ctg}\nolimits} 30^\circ = r\sqrt 3 \cdot \sqrt 3 = 3r.$

По условию площадь прямоугольника ${S_{ABCD}} = BA \cdot AD = 3r \cdot r\sqrt 3 = 3\sqrt 3 {r^2} = 4\sqrt 3 ,$ откуда

${r^2} = \displaystyle\frac{4}{3}.$

Полная поверхность цилиндра с радиусом основания $r$ и высотой $h$ определяется по формуле $S = 2\pi r(r + h).$

В этой задаче $h = BA = 3r$, поэтому $S = 2\pi r(r + 3r) = 2\pi r \cdot 4r = 8\pi {r^2} = 8\pi \cdot \displaystyle\frac{4}{3} = \displaystyle\frac{{32}}{3}\pi \approx \displaystyle\frac{{32}}{3} \cdot 3{,}14 = 33{,}49.$

#SPJ1