Предмет: Математика,
автор: maxliyoyavkochova
помогите пожалуйста
Приложения:
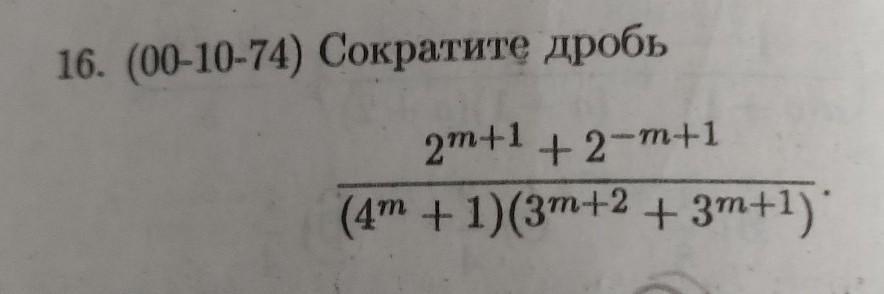
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Сократить дробь:
Воспользуемся правилами:
Вынесем в числителе общий множитель 2 и сократим дробь:
И еще одно правило понадобится:
Похожие вопросы
Предмет: Українська мова,
автор: starovski
Предмет: Русский язык,
автор: maxim3214202
Предмет: Русский язык,
автор: Лера3425635
Предмет: Русский язык,
автор: adam007f