Предмет: Математика,
автор: albina1980ab
ПЖ ПОМОГИТЕ ОЧЕНЬ СРОЧНО
Приложения:
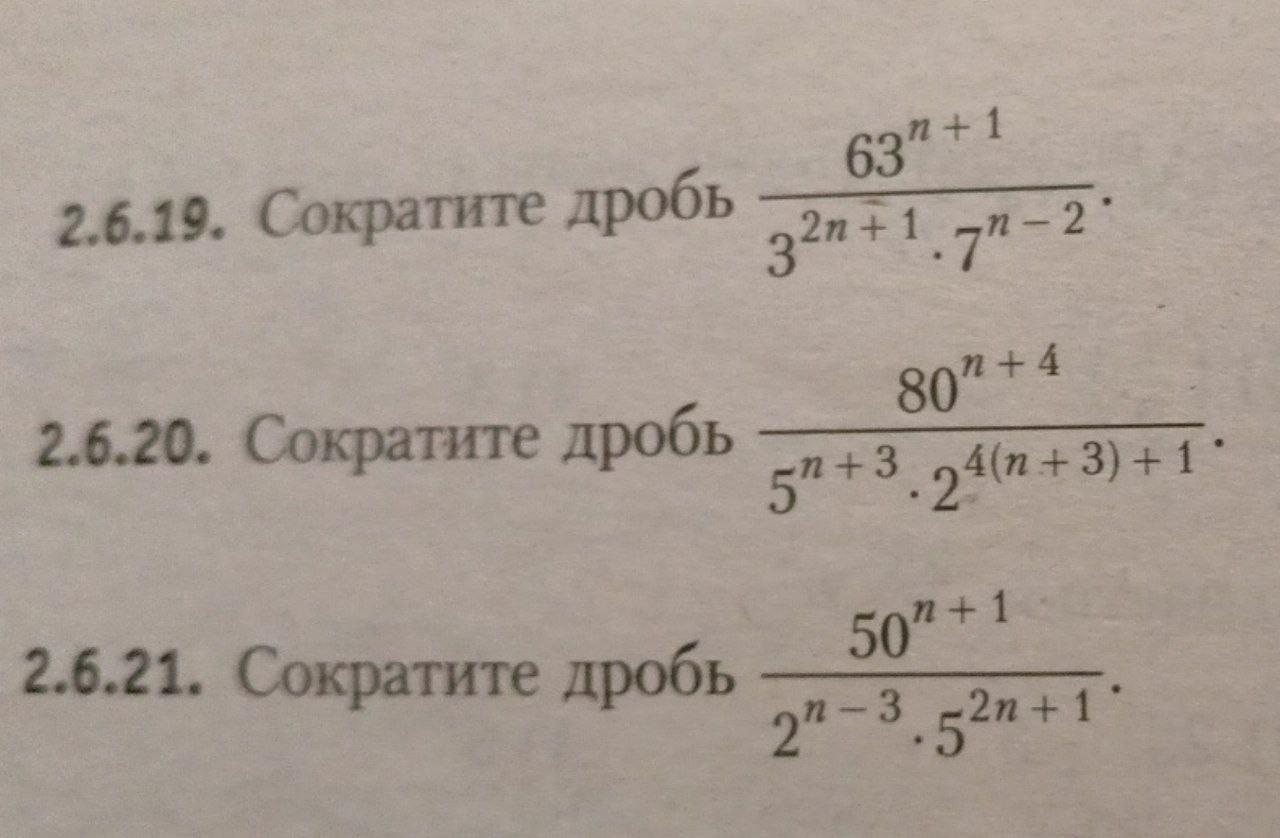
Ответы
Автор ответа:
1
Ответ:
2.6.19. 1029;
2.6.20. 40;
2.6.21. 80
Пошаговое объяснение:
Воспользуемся свойствами степени
2.6.19.
2.6.20.
2.6.21.
Автор ответа:
1
Решение.
Применяем свойства степеней :
Похожие вопросы
Предмет: Английский язык,
автор: анж45
Предмет: Русский язык,
автор: лизсон
Предмет: Русский язык,
автор: Milka2006mail
Предмет: Русский язык,
автор: protosei14
Предмет: Математика,
автор: Nastis123