Предмет: Математика,
автор: svinka114
Решить неравенство. Кто-нибудь может помочь?
Приложения:
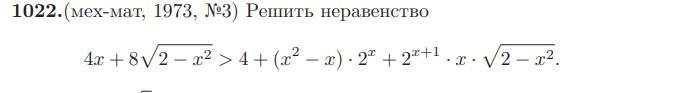
antonovm:
(-1 ; корень из 2 ] , без вас мне бы на этом сайте было скучно
решение позже
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Рассмотрим на ОДЗ
При отрицательных значения аргумента очевидно положительна.
При положительных значениях аргумента функции и
возрастающие, поэтому их произведение тоже возрастает, а
— убывает. Значение в правом конце ОДЗ
т. к.
Значит и при положительных аргументах из ОДЗ
Поэтому задача сводится к решению неравенства
Автор ответа:
1
Ответ:
//////////////////////////////////////////////
Пошаговое объяснение:
Приложения:
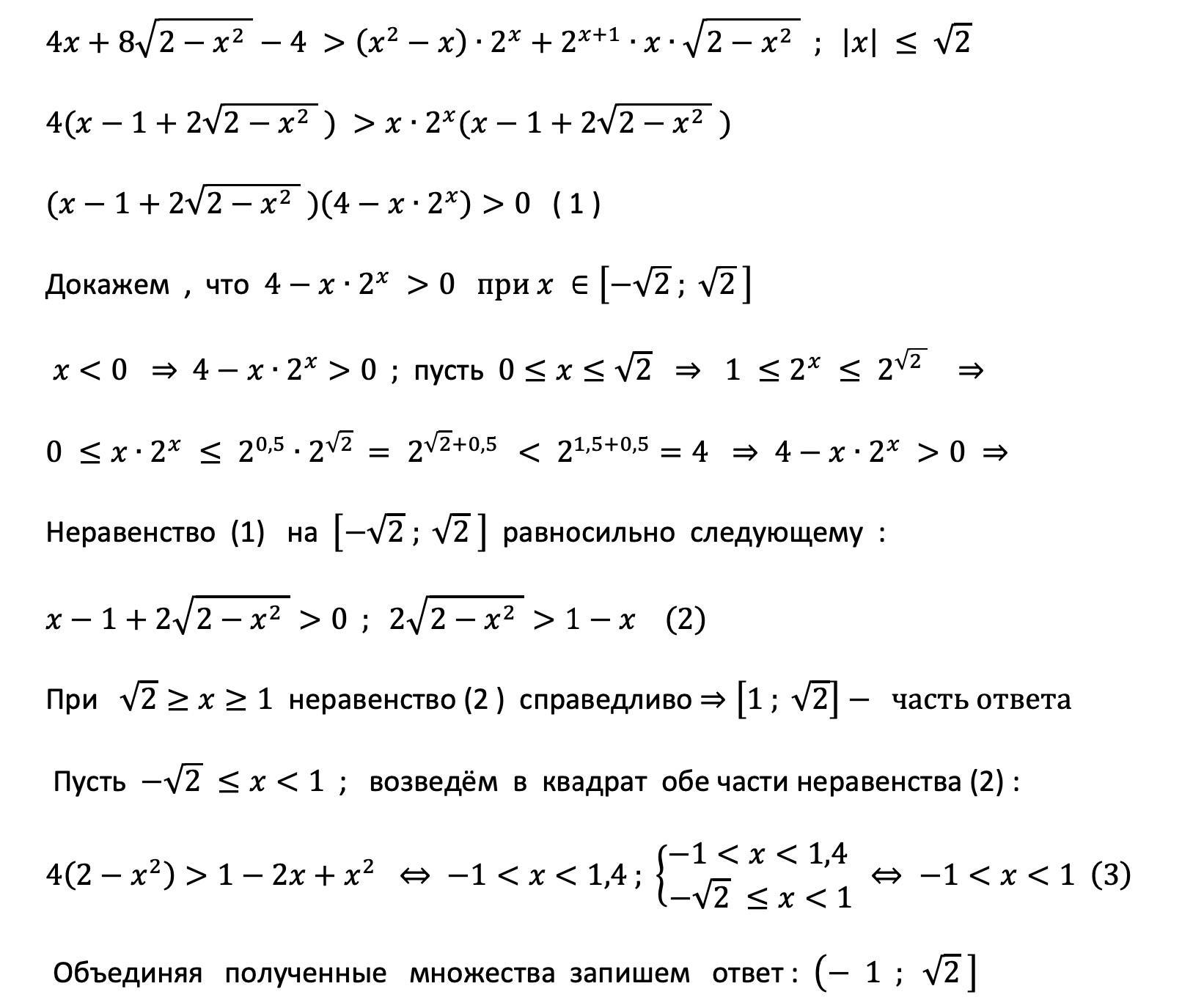
Похожие вопросы
Предмет: Русский язык,
автор: MissHalsey
Предмет: Русский язык,
автор: тагуи4
Предмет: Русский язык,
автор: кэти62
Предмет: История,
автор: leykaUss
Предмет: Русский язык,
автор: noname7480