Question

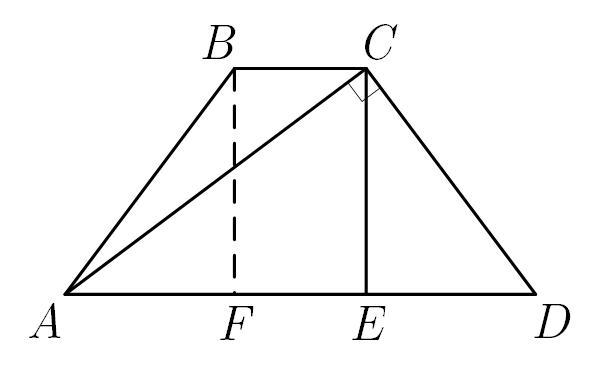
Знайдіть периметр рівнобедреної трапеції, основи якої дорівнюють 7 см і 25 см, а діагоналі перпендикулярні до бічних сторін.​

Answer 1

Ответ:

$P=62$

Объяснение:

Опустим высоты $BF$ и $CE$ на нижнее основание. Тогда

$AF = ED = \displaystyle\frac{{AD - BC}}{2} = \displaystyle\frac{{25 - 7}}{2} = 9,$

а

$AE = AF + FE = AF + BC = 9 + 7 = 16.$

В прямоугольном треугольнике $ACD$ высота, проведенная к гипотенузе, вычисляется как $CE = \sqrt {AE \cdot ED} = \sqrt {16 \cdot 9} = 12.$

Значит из треугольника $CED$ по теореме Пифагора

$CD = AB = \sqrt {{9^2} + {{12}^2}} = 15.$

Периметр трапеции

${P_{ABCD}} = AB + BC + CD + AD = 15 + 7 + 15 + 25 = 62.$

Answer 2

Ответ:

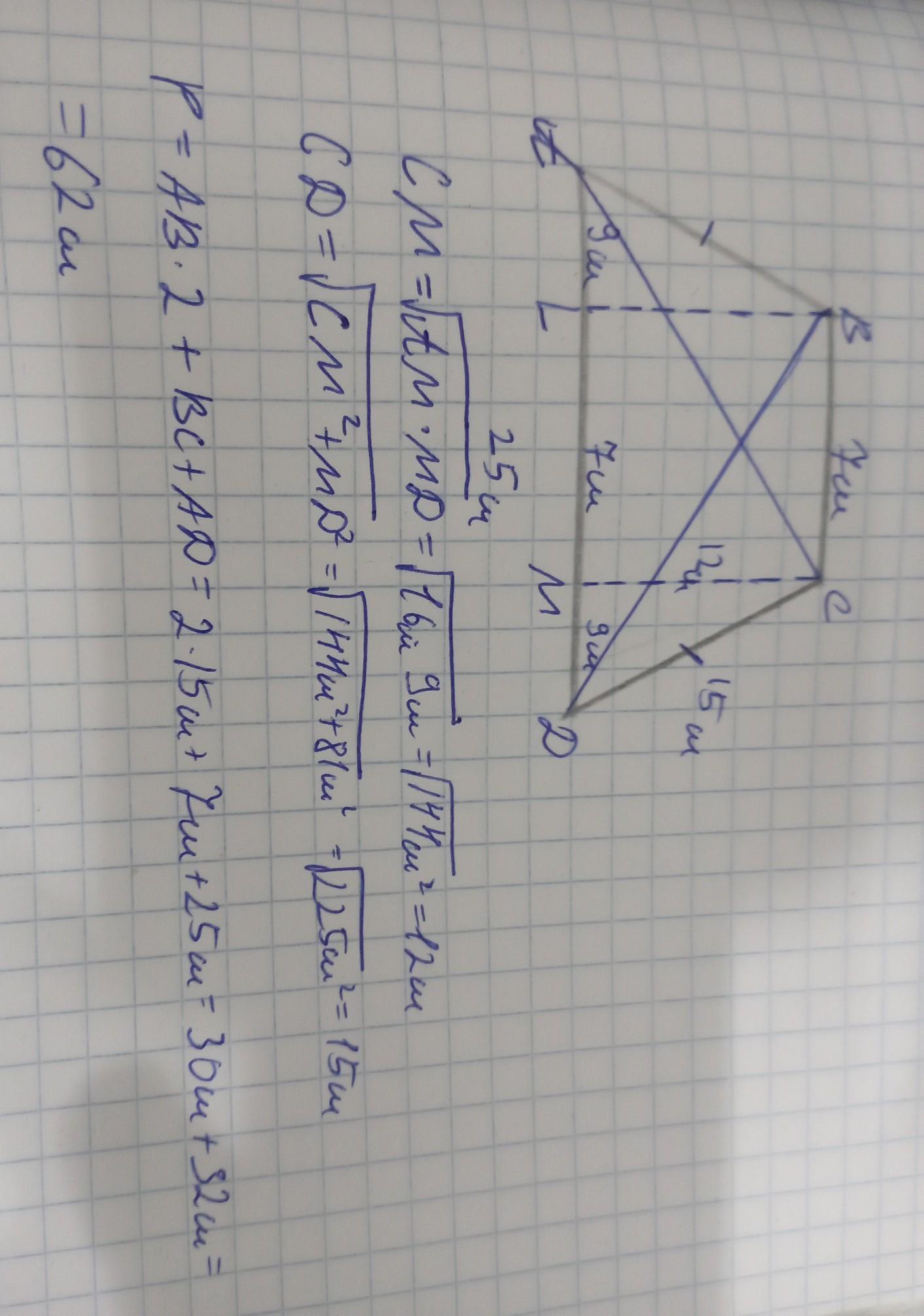
держи

===================