Предмет: Математика,
автор: Аноним
ПРОШУ В ВАС ДОПОМОГИ
Приложения:
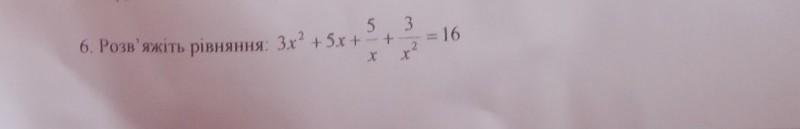
mugiwaranoluffy:
(-11 ±√85)/6
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Перегруппируем слагаемые:
Сделаем замену тогда
т. е.
Перепишем уравнение:
Сделаем обратную замену:
либо
Похожие вопросы
Предмет: Русский язык,
автор: ДаШаГО
Предмет: Русский язык,
автор: Olya545
Предмет: Немецкий язык,
автор: джинджина
Предмет: Алгебра,
автор: yaroslwv0511
Предмет: Физика,
автор: annaslas6684