Question

помогите пожайлуста решить задачу!!!​

Answer 1

Ответ:

18.47

Объяснение:

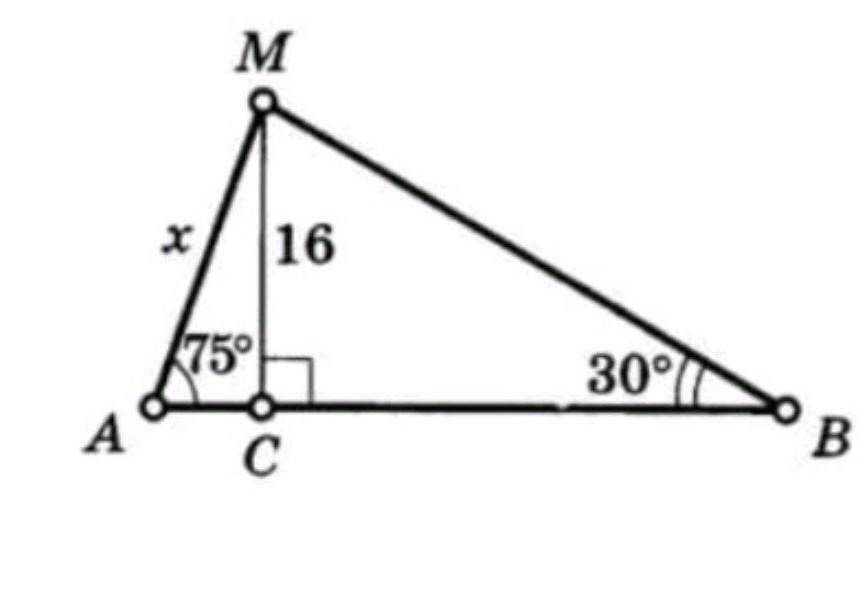
Рассмотрим треугольник ΔМСB - прямоугольник , ∠CMB = 180° - 90° - 30° = 60°

За теоремой про синусы, BC/sin60° = MC / sin 30°

BC/ √3 : 2 = 16 / 0.5

BC = 16√3

Проекция треугольника

MC^2=AC*CB

16^2=AC*16√3

AC = 16 √3 : 3

AB = 16 √3 : 3 + 16√3 = 64 √3 : 3

За теоремой про синусы

MB / sin 90° = MC / sin 30°

MB / 1 = 16 / 0.5

MB = 32

За теоремой Пифагора:

AB^2=AM^2+MB^2

AM^2=AB^2-MB^2

AM^2= ( 64 √3 : 3 )^2 -  1024 =  4096 : 3 - 1024 = 341.3

AM = √341.3

AM = 18.47

Answer 2

Ответ:

$x=16(\sqrt 6 - \sqrt 2 )$

Объяснение:

$\angle CMB = 90^\circ - 30^\circ = 60^\circ , \angle AMC = 90^\circ - 75^\circ = 15^\circ .$

Тогда $\angle AMB = \angle CMB + \angle AMC = 60^\circ + 15^\circ = 75^\circ ,$

т. е. треугольник $AMB$ равнобедренный.

Из треугольника $MCB$ с углом $30^\circ$  $MB = AB = 32,$ а

$BC = \displaystyle\frac{{16}}{{{\mathop{\rm tg}\nolimits} 30^\circ }} = 16:\displaystyle\frac{1}{{\sqrt 3 }} = 16\sqrt 3 .$

Тогда по теореме Пифагора из треугольника $ACM$

$AM = \sqrt {{{16}^2} + {{(32 - 16\sqrt 3 )}^2}} = 16\sqrt {1 + {{(2 - \sqrt 3 )}^2}} = 16\sqrt {1 + 4 - 4\sqrt 3 + 3} =\\\\= 16\sqrt {8 - 4\sqrt 3 } = 16\sqrt {2(4 - 2\sqrt 3 )} = 16\sqrt {2({{(\sqrt 3 )}^2} - 2\sqrt 3 + 1)} =\\\\= 16\sqrt {2{{(\sqrt 3 - 1)}^2}} = 16(\sqrt 3 - 1)\sqrt 2 = 16(\sqrt 6 - \sqrt 2 ).$