Предмет: Геометрия,
автор: Varjaaa
Вычислите площадь криволинейной трапеции на рисунках 1, 3, 4, 5, 6
Приложения:
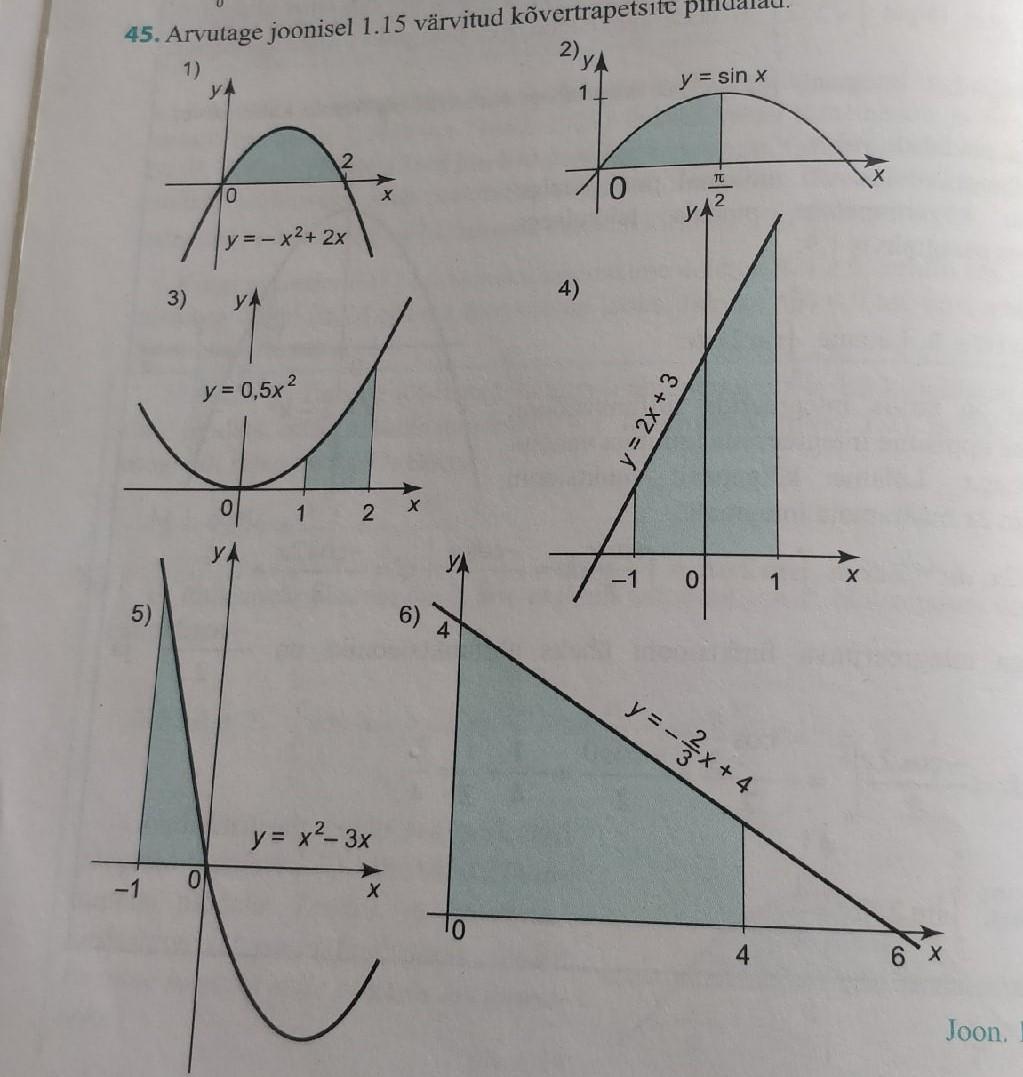
Ответы
Автор ответа:
0
Ответ:
Площадь криволинейной трапеции :
Похожие вопросы
Предмет: Английский язык,
автор: LaaLaaLaand
Предмет: Русский язык,
автор: 891152717111
Предмет: Русский язык,
автор: Аноним
Предмет: Физика,
автор: nastya2k02
Предмет: Литература,
автор: amir008