Предмет: Геометрия,
автор: kropivkaa07
Центр кола, описаного навколо рівнобічної трапеції, лежить на більшій
основі. Відрізки, на які ділить діагональ трапеції висоту, проведену з
вершини тупого кута, дорівнюють 21 см і 27 см, починаючи від більшої
основи. Знайдіть периметр трапеції.
cos20093:
R = 6*23/√7; a = 12*23/√7; b = 12*9/√7; (a - b)/2 = 6*14/√7; иногда проще тащить выражения в таком виде, и только в конце убирать сомножители и избавляться от корня в знаменателе. У меня получилось c = 12√23, но я уже ни в чем не уверен :) Ну, как считать я рассказал, попробуйте сами проделать все это. Другой способ. Если продлить высоту, сделав из неё хорду, то (a+b)(a - b)/4 = 27*(21+48) = 27*69; уже было (a-b)/(a+b)=7/16; система простая, попробуйте так сосчитать.
Что-то у меня с головой сегодня :)))) (a+b)(a - b)/4 = 48*48; не, я на сегодня все :))
С утра я все-таки досчитал. Ответ 24√23 + 384√7/7; короче всего оказался способ из моего комментария выше. Напомню, получается (a-b)/(a+b)=7/16; (a+b)(a-b)=96²; => (a-b)²=7*6²*16; a-b=24√7; далее, из первого уравнения 23b=9a; => a = 12*23√7/7 = 276√7/7; b=108√7/7; боковая сторона c²=48²+(12√7)²=12²*(16+7); c = 12√23; ну и сложить a + b + 2c;
Если вы страдаете бессонницей и в промежутке между тупыми сериалами в полусне решаете мутные вычислительные задачи для школьников, лучше делать это утром на свежую голову. :))
Я подумал, а почему бы не вспомнить на минутку, что у меня высшее образование, да еще и - не слабое. Пусть высота трапеции h, а нижний её отрезок m (m=21); тогда (a-b)/(a+b)=m/h; напомню, это получается из подобия треугольников, образованных высотами, диагональю и большим основанием. (a+b)(a-b)=4h²; это потому, что большее основание - диаметр, он делит хорду, частью которой является высота, пополам, а сам делится на отрезки (a-b)/2 и (a+b)/2;
В таком "буквенном" виде счет на удивление прост. (a-b)²=4mh; c² = h²+(a-b)²/4 = h²+mh; (a+b)² = 4h³/m; P = a+b +2c = 2(h/m)√(hm) + √((h+m)h); это все. Остается подставить h = 48, m=21, и легко получается ответ.
Я намеренно записал в таком виде (можно было немного меньше скобок) - там сразу просматриваются √(hm) = √(48*21) = 12√7 (вот и корень из 7) и точно также √((h+m)h) = √(69*48) = 12√23; Кстати, я там множитель 2 пропустил перед последним корнем (надо 2c)
Кстати, эту форму ответа ("в буквах") еще можно упростить (или сделать "красивее"). Если положить m/h = k, то ответ принимает вид P=2h(√k/k + √(k+1) )
В данном случае k = 7/16, P = 96(4√7/7+√23/4), проверьте, что это совпадает с ответом :)
Ну, я все равно тут простыню написал, модераторы потом вычистят :) Поэтому не могу отказать себе набрать окончательный вариант расчета. (a-b)/(a+b)=m/h =k; (a+b)(a-b)=(2h)²; => a+b = 2h/√k (просто поделил второе на первое и извлек корень), (a-b)²=(2h)²k; c² = h²+(a-b)²/4 = h²(1+k); P = a+b+2c = 2h(√k/k + √(k+1)); При k = 7/16; P=96(4√7/7+√23/4) = 384√7/7+24√23;
Ответы
Автор ответа:
0
Ответ:
Периметр трапеции равен
Объяснение:
По условию
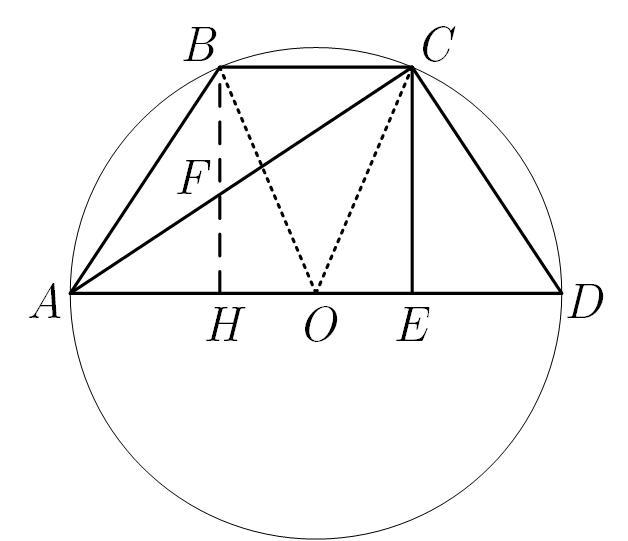
Пусть большее основание трапеции равно , а меньшее —
. Если провести вторую высоту трапеции
, то
,
Треугольники и
подобны, откуда
Тогда
Треугольник — прямоугольный (описанная вокруг трапеции окружность описана и около этого треугольника, его угол
опирается на диаметр окружности), поэтому
откуда
По теореме Пифагора из треугольника
Тогда периметр трапеции
Приложения:
Автор ответа:
0
1) перегляньте умову (ви вже знаєте , що у цьому збірнику купа описок)
2) подивіться, може ви самі невірно написали 21 і 27, а треба 27 і 21.
3) Яка відповідь до цієї задачі у збірнику.
Розв'язання по вашій умові і червоним стисло , якщо в умові все ж таки "27 і 21 починаючи від більшої основи".
Приложения:


Давайте дофантазируем дальше и предположим, что там числа 24 и 20. Может же быть такая описка? Почему бы не решить и такую задачу?
Може бути все що завгодно. Тому і питання до kropivkaa07. Я все конкретно запитала. Чи не можна? А оскільки реакції ще не було, то нема про що і говорити. Є три розв'язання даної задачі. Яку захоче таку і перепишемо, якщо все одно.
Почему у нас получились разные ответы, вот в чем вопрос :)
У нас с уважаемым комментатором cos20093 ответы совпали, а у вас корень из 161
Треба ще раз переглянути. Я не дивилися ні ваше, ні в коментах ще одне, щоб предметно щось сказати. Може автор питання з'явиться.
А я всегда читаю ваши решения. У вас красиво
Значить може десь технічна помилка. Буде час подивлюся, зараз просто не хочеться повертатися до цієї задачі. Знайду, направлю модератору, щоб поставив опцію "виправити на прохання".
Вы посмотрите мой последний комментарий наверху, я думаю у вас все сомнения отпадут.
GoldenVoice. Ще раз переглянула , розв'язання доволі просте і прозоре: подібність, теор. Піф, метричні співвідношення, все що для 8 класу. (автор у 8 класі) Відповідь вірна. Але вірна і у вас. Поосто гра чисел. Ірраціональне число записане по-різному , якщо записати десятковим дробом, то це 260,238...
Спасибо, разобрались :)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: lllbeback
Предмет: Қазақ тiлi,
автор: Шанн1985
Предмет: Английский язык,
автор: coolsollo
Предмет: Математика,
автор: haila
Предмет: История,
автор: aniks54