Question

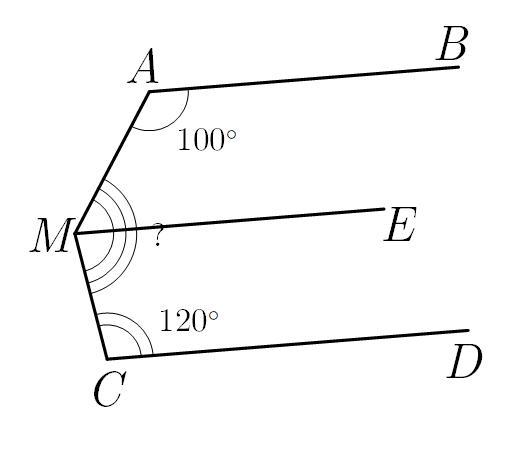
На малюнку 43 прямі АВ і СД паралельні. Знайдіть градусну міру кута АМС.​

Answer 1

Ответ:

∠АМС =  140°

Объяснение:

Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.

S= 2d(n - 2),         формула (1)

где S — это сумма углов,

      2d — два прямых угла (то есть 2 · 90 = 180°),

      n — количество сторон.

Проведем перпендикуляр BD к сторонам  АВ и СD. ( АВ ║СD)

Мы получим выпуклый многоугольник - пятиугольник.

Мы знаем все углы, кроме ∠АМС и знаем сумму углов.

∠ABD и ∠BDC  - прямые, мы так построили.

Тогда сумма углов будет равна

S = 2*90° + 100° + 120° + ∠AMC = 400° + ∠AMC

С другой стороны,  по приведенной выше формуле (1)  (n =5)

S = 180°(n - 2) = 180° * 3 = 540°

Таким образом,

540° = 400° + ∠АМС

И тогда

∠АМС = 540° - 400° = 140°

Answer 2

Ответ:

$\angle AMC=140^\circ$

Объяснение:

Проведем через точку $M$ прямую $ME$ параллельно прямым $AB$ и $CD$.

Тогда углы $AME$ и $MAB$ внутренние односторонние при параллельных прямых, т. е. в сумме дают $180^\circ$. Значит

$\angle AME=180^\circ-100^\circ=80^\circ.$

Точно так же внутренними односторонними при параллельных прямых являются углы $EMC$ и $MCD$. Значит

$\angle EMC=180^\circ-120^\circ=60^\circ.$

Тогда

$\angle AMC=\angle AME+\angle EMC=80^\circ+60^\circ=140^\circ.$