Question

C - медиана прямоугольного треугольника, а O - центр вписанной окружности. AC = 3, BC = 4. Найти угол AOB. Найти площадь треугольника AOB.

Answer 1

Центр вписанной окружности - точка пересечения биссектрис.

△ABC: A/2 +B/2 +C/2 =90°

△AOB: A/2 +B/2 +∠AOB =180°

=> ∠AOB =90° +C/2

Доказали:

В любом треугольнике угол между биссектрисами равен 90° + половина третьего угла.

∠AOB =90° +C/2 =90°+45° =135°

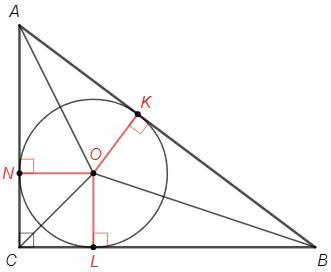
Проведем радиусы OK=OL=ON=r в точки касания. Они перпендикулярны касательным и являются высотами в треугольниках AOB, BOC, AOC.

S(ABC) =S(AOB)+S(BOC)+S(AOC) =1/2 r (AB+BC+AC) =pr (p-полупериметр)

Доказали: S△=pr

S(ABC) =3*4/2 =6

p(ABC)=(3+4+5)/2 =6

S=pr => r=1

S(AOB) =1/2 AB*OK =5/2 =2.5