Помогите пожалуйста, умоляю и ноги целую
Завтра сдавать репетитору а я забыл как решать
Если можно все 4 и с подобным решением
Даю 60 баллов
Тот кто решит за того молиться буду
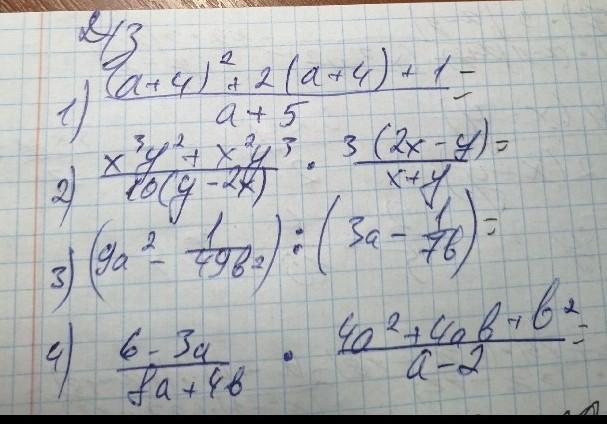
Ответы
Пример 1)
Разберёмся сначала с числителем:
Для наглядности сделаем замену :
(мы использовали формулу квадрата суммы в обратную сторону)
Подставим:
При этом мы должны записать ОДЗ , чтобы не получилось деление на ноль.
Пример 2)
(перед тем, как сокращать, мы должны записать ОДЗ: и
, чтобы не получилось деление на ноль):
Пример 3)
(перед тем, как сокращать, мы должны записать ОДЗ: и
, то есть
, чтобы не получилось деление на ноль):
Пример 4)
(в числителе второй дроби записано разложение квадрата суммы , поэтому получим следующее):
(перед тем как сокращать, мы должны записать ОДЗ: и
, чтобы не получилось деление на ноль):
Если что-нибудь непонятно — спрашивай.
P. S. Помолись не за меня, а чтобы война закончилась.
Розв'язання завдання додаю.
В першому не треба ніякої заміни. Як би було рівняння, то так, заміна. А в простих виразах , як цей, краще розкривати дужки .
