Предмет: Геометрия,
автор: egrgwgwgw
Срочно, даю 40 баллов
Приложения:
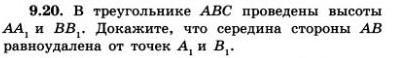
Ответы
Автор ответа:
0
Ответ:
Доказано, что середина стороны АВ равноудалена от точек А₁ и В₁.
Объяснение:
9.20. В треугольнике ABC проведены высоты AA₁ и BB₁. Докажите, что середина стороны АВ равноудалена от точек А₁ и В₁.
Дано: ΔАВС;
М - середина АВ;
АА₁ и ВВ₁ - высоты.
Доказать: МА₁ = МВ₁
Доказательство:
1. Рассмотрим ΔАВВ₁ - прямоугольный.
АМ = МВ (условие)
⇒ В₁М - медиана.
- Медиана, проведенная из вершины прямого угла к гипотенузе, равна половине гипотенузы.
⇒ (1)
2. Рассмотрим ΔАВА₁ - прямоугольный.
АМ = МВ (условие)
⇒ А₁М - медиана.
(2)
В равенствах (1) и (2) правые части равны, значит равны и левые.
Доказано, что середина стороны АВ равноудалена от точек А₁ и В₁.
Приложения:
Похожие вопросы
Предмет: Технология,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: sashalyubumenko
Предмет: Алгебра,
автор: mrhjhvfdcv