мне очень нужна ваша помощь. нужно решить все 3
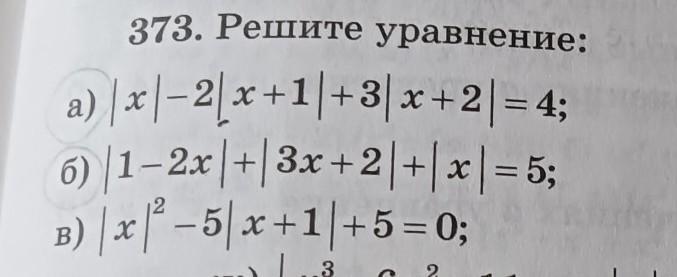
Ответы
Ответ:
а)
б)
в)
Пошаговое объяснение:
а) Найдем точки, в которых модули превращаются в ноль: ;
,
и
,
.
Разобьем числовую прямую этими точками на четыре промежутка. На каждом из этих промежутков знак каждого из подмодульных выражений постоянен, что позволяет нам раскрыть модули по определению:
I.
Так как , найденное значение является корнем уравнения.
II.
Так как , то на данном промежутке уравнение корней не имеет.
III.
Получили тождественно верное равенство, значит все числа из промежутка являются корнями данного уравнения.
IV.
Так как , то значение
является корнем данного уравнения.
Собирая найденные ответы, получаем:
б) Модули превращаются в ноль в точках
и
которые разбивают числовую прямую на четыре промежутка.
I.
Так как найденное число является корнем уравнения.
II.
Так как в результате получили ложное равенство, на данном промежутке уравнение не имеет корней.
III.
Так как на данном промежутке уравнение не имеет корней.
IV.
Так как то найденное число является корнем уравнения.
Собирая найденные ответы, получаем:
в) Так как , достаточно рассмотреть два промежутка, на которые числовую прямую разбивает точка
.
I.
На данном промежутке уравнение не имеет корней
II.
Оба числа больше , поэтому являются корнями данного уравнения.