Предмет: Математика,
автор: bezobrazie228
помогите с примером пожалуйста)
Приложения:
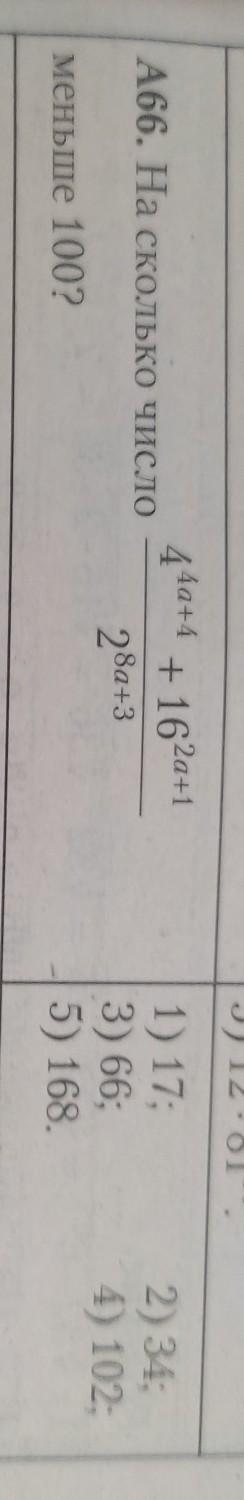
Ответы
Автор ответа:
1
Ответ:
3) 66.
Пошаговое объяснение:
На сколько число
меньше 100?
Преобразуем данное выражение. Для этого каждое выражение представим в виде степени с основанием 2.
При возведении степени в степень основание остается прежним, а показатели перемножаются .
При делении степеней с одинаковыми основаниями основание остается прежним а из показателя делимого вычитается показатель делителя.
Найдем на сколько полученное число 34 меньше 100.
100 - 34 = 66
И тогда получаем 3) 66.
Приложения:

bezobrazie228:
спасибо! отличный ответ
Похожие вопросы
Предмет: Другие предметы,
автор: Андре41
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: znad
Предмет: Математика,
автор: AmirOWhite
Предмет: Другие предметы,
автор: misha2305wot