Question

Площа ривнобедренного трикутника з кутом при основи 30 доривнюэ 64 корень из 3 см^2 Знайдить стороны трикутника

Answer 1

Відповідь

розв'язання завдання додаю

Answer 2

Ответ:

Так, як ΔАВС рівнобедрений позначимо бокові сторони, як х, а кут між ними: 180-(30*2)=180-60=120°

Площа трикутника знаходиться по формулі:

SΔ=(1/2)*х*х*sin120°=(1/2)*х² *(√3/2)

64√3=(1/2)*х² *(√3/2)

64√3=(√3/4)*х²

х²=256

х=16

АВ=ВС=16 см

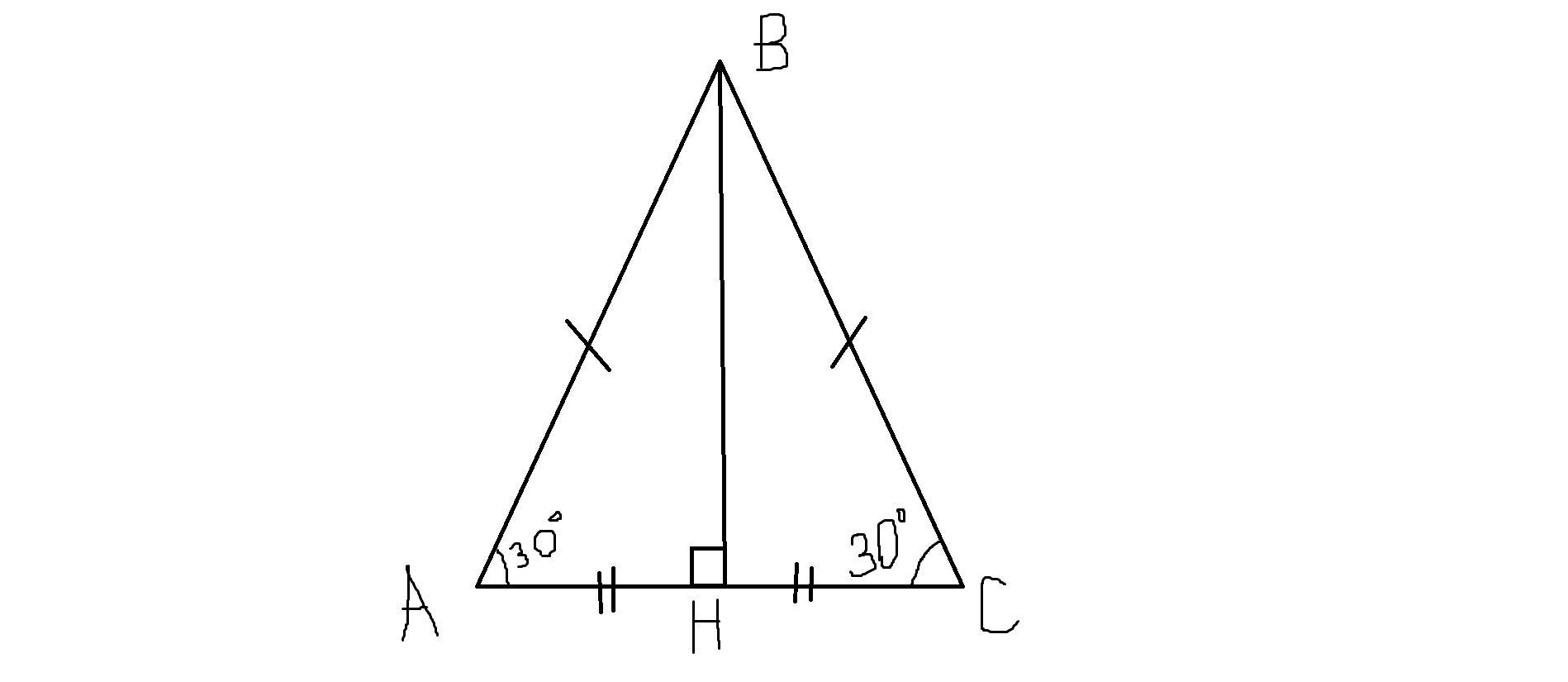
Побудуємо висоту ВН, отримаємо прямокутний ΔАВН

За опорним фактом: ВН=1/2АВ=1/2*16=8 (см)

За теоремою Пифагора знайдемо АН:

АН=√(АВ²-ВН²)=√(16²-8²)=√(256-64)=√192=8√3 (см)

АС=2АН=(8√3)*2=16√3 (см)

Відповідь: сторони трикутника 16, 16 и 16√3.