Предмет: Алгебра,
автор: Tiffanyevgenia
Помогите полжалуйста
Приложения:

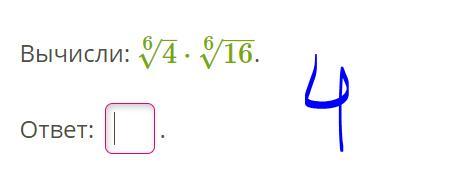
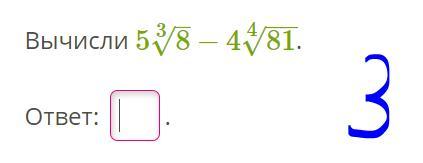

Ответы
Автор ответа:
1
Ответ:
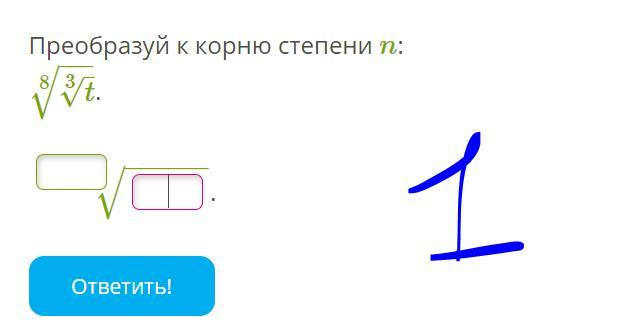
1. ;
2. ;
3. –2;
4. 2;
5. 0,15
Объяснение:
1. поэтому
2.
Поэтому
3.
4. Воспользуемся тем, что ,
и \sqrt[{2k}]
5. Воспользуемся тем, что
Похожие вопросы
Предмет: Французский язык,
автор: ROMsathif
Предмет: Русский язык,
автор: Ulnaaaaaaaaaaa
Предмет: Английский язык,
автор: Larashalll73
Предмет: Қазақ тiлi,
автор: anastasia6298
Предмет: Русский язык,
автор: alissa333pitnechenko