Question

помогите пж с заданиями!!!​

Answer 1

Ответ:

во вложении

===================

Answer 2

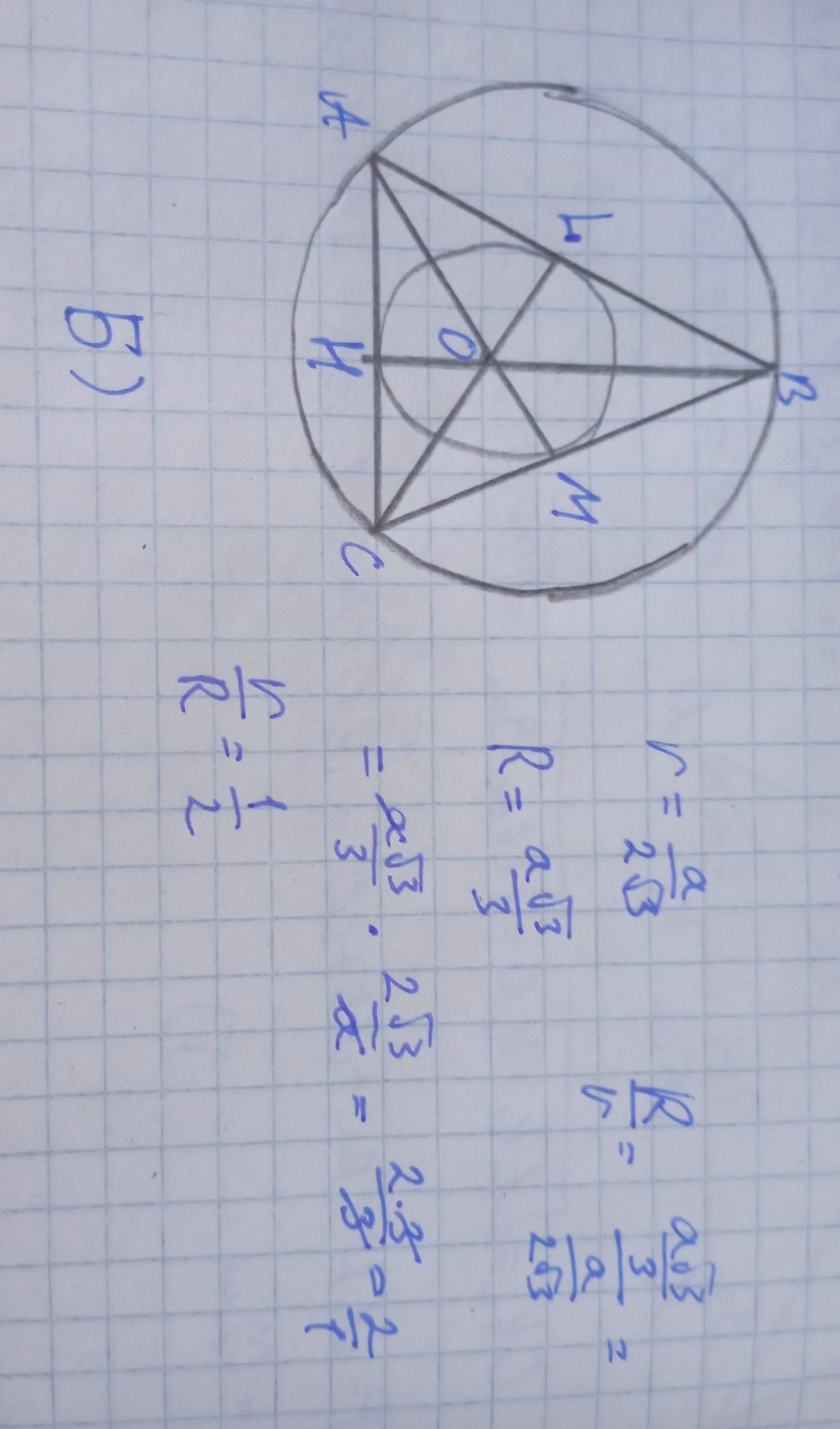
Ответ:

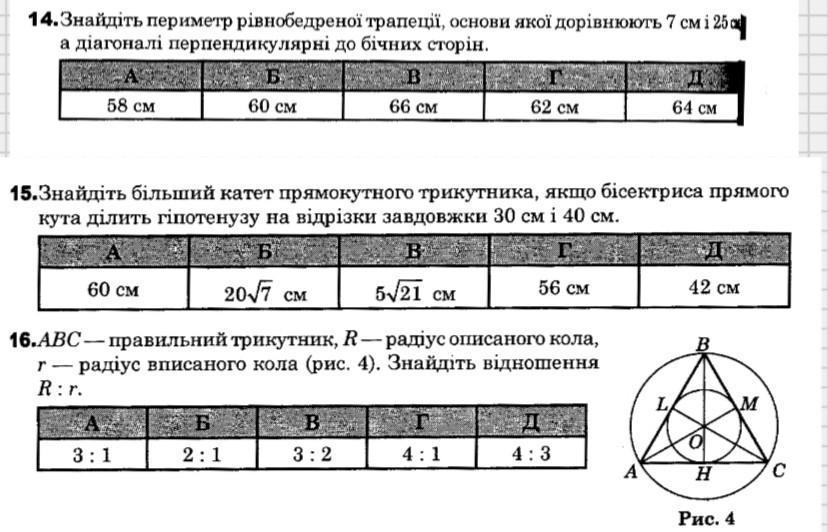
14. Г. 15. Г. 16. Б

Объяснение:

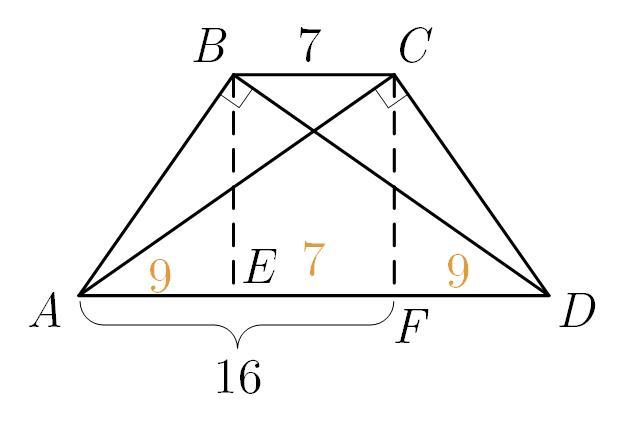
14. Опустим из вершин $B$ и $C$ высоты $BE$ и $CF$ на нижнее основание (см. рис.). Тогда $BCFE$ — прямоугольник, $BC = EF = 7.$ Так как трапеция равнобокая, то отрезки $AE$ и $FD$ равны и каждый из них равен

$\displaystyle\frac{{25 - 7}}{2} = 9.$

Тогда $AF = AE + EF = 9 + 7 = 16.$

Найдем высоту в прямоугольном треугольнике $ACF,$ используя формулу

$CF = \sqrt {AF \cdot FD} = \sqrt {16 \cdot 9} = 4 \cdot 3 = 12.$

Тогда по теореме Пифагора из треугольника $CFD$

$AB = CD = \sqrt {C{F^2} + F{D^2}} = \sqrt {{{12}^2} + {9^2}} = \sqrt {144 + 81} = \sqrt {225} = 15.$

Значит периметр трапеции

$P = AB + BC + CD + AD = 15 + 7 + 15 + 25 = 62.$

15. Биссектриса угла делит противоположную сторону на отрезки, пропорциональные прилегающим сторонам. Тогда катеты треугольника пропорциональны числам 30 и 40, значит относятся друг к другу как

$\displaystyle\frac{{30}}{{40}} = \displaystyle\frac{3}{4}.$

Пусть один катет равен $3x,$ тогда второй (больший) $4x,$ а гипотенуза равна $30 + 40 = 70.$

По теореме Пифагора

${(3x)^2} + {(4x)^2} = {70^2};\\\\9{x^2} + 16{x^2} = 4900;\\\\25{x^2} = 4900;\\\\{x^2} = 196;\\\\x = 14.$

Значит больший катет треугольника равен $4 \cdot 14 = 56.$

16. В равностороннем треугольнике центр вписанной и описанной окружностей совпадают. Так как т. $O$ в том числе и точка пересечения медиан, каждый из отрезков $AM,$ $BH$ и $CL$ точкой $O$ делится в отношении $2:1,$ считая от вершины. Тогда

$\displaystyle\frac{2}{3}BH = R,$ $\displaystyle\frac{1}{3}BH = r,$

а их отношение $R:r = 2:1.$