Question

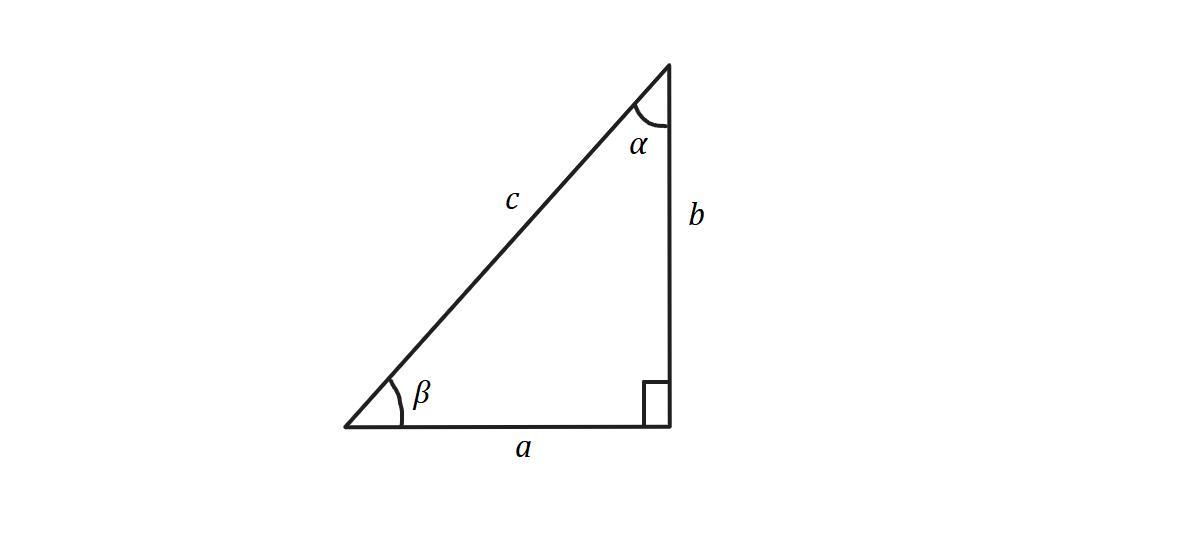
решите прямоугольный треугольник​

Answer 1

Имеем: один прямой угол, и два острых угла ($\alpha$ и $\beta$).

a,b - катеты, c - гипотенуза.

Прямой угол = 90°.

Из теории, сумма двух острых углов = 90°.

Из условия, нам дан угол $\beta$, через него находимо угол $\alpha$:

$\alpha$=90°-$\beta$ => $\alpha$=90°-27°=63°.

Находим гипотенузу (c) через соотношение:

$\displaystyle\mathsf{cos\alpha =\frac{b}{c} }$                  

cos(63°)=50/c

cos(63°)*c=50

c=50/(cos(63°))≈110,13446≈110.

Находим катет а через соотношение:

$\displaystyle\mathsf{tg\alpha =\frac{a}{b} }$

tg(63°)=a/50

a=50*tg(63°)≈98,13053≈98.

Итого, ответ:

a≈98.

b=50.

c≈110.

$\alpha =63$°.

Answer 2

Ответ:

$a \approx 98,\ c \approx 111{,}1,\ \alpha = 63^\circ$

Пошаговое объяснение:

Действительно, так как треугольник прямоугольный, то сумма его острых углов равна $90^\circ .$

Значит $\alpha = 90^\circ - \beta = 90^\circ - 27^\circ = 63^\circ .$

Через метрические соотношения в прямоугольном треугольнике

$\sin \beta = \displaystyle\frac{b}{c},\ {\mathop{\rm ctg}\nolimits} \beta = \displaystyle\frac{a}{b},$

откуда

$c = \displaystyle\frac{b}{{\sin \beta }},\ a = b{\mathop{\rm ctg}\nolimits} \beta .$

С использованием калькулятора найдем, что

$\sin 27^\circ \approx 0{,}45,\ {\mathop{\rm ctg}\nolimits} 27^\circ \approx 1{,}96.$

Тогда

$c \approx \displaystyle\frac{{50}}{{0{,}45}} \approx 111{,}1,\ a \approx 50 \cdot 1{,}96 = 98.$