Предмет: Математика,
автор: bezobrazie228
не понимаю как решать
Приложения:
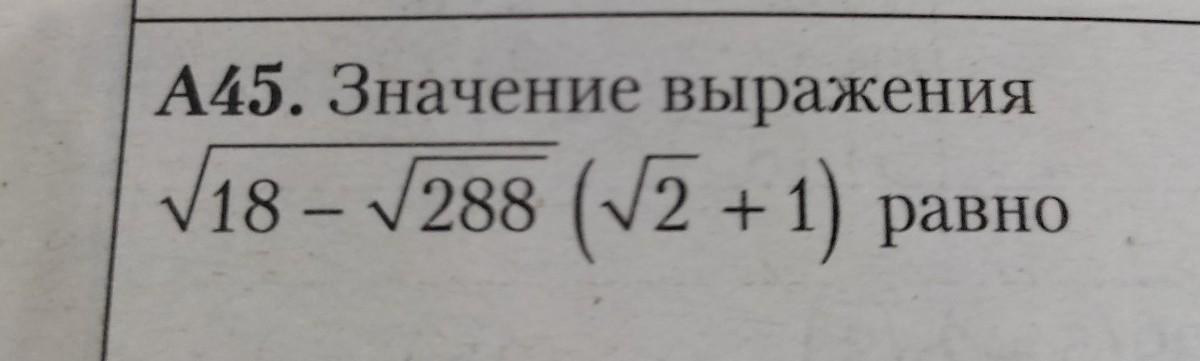
aarr04594:
Зручно позбутися виразу в дужках, домножив на пов'язаний з ним вираз, отримаємо 1. Але не забути і поділити. Під один корінь , скорочення і корінь з шести.
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Тогда под корнем
Результат произведения
благодарю
Автор ответа:
1
Ответ:
√6.
Пошаговое объяснение:
√(18 - √288) • (√2 + 1) =
= √(18 - √(2•144)) • (√2 + 1) =
= √(18 - 12√2) • (√2 + 1) =
= √6•√(3 - 2√2) • (√2 + 1) =
= √6 • √(3 - 2√2) • √(√2 + 1)² =
= √6 • √(3 - 2√2) • √((√2)² + 2√3•2 + 1²) =
= √6 • √(3 - 2√2) • √(3 + 2√2) =
= √6 • √(3² - (2√2)²) = √6 • √(9-8)=
= √6 • √1 = √6.
Похожие вопросы
Предмет: Русский язык,
автор: меййси
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: NikiKrou
Предмет: ОБЖ,
автор: pastahaev
Предмет: Право,
автор: Sviridova1609n