Предмет: Геометрия,
автор: Grut09797
Основи трапеції дорівнюють а і b (a>b), кути при більшій основі дорівнюють 30º і 45°. Знайти площу трапеції. Відповідь: (√3 −1)(b² -a²)/4
Приложения:
BMW52:
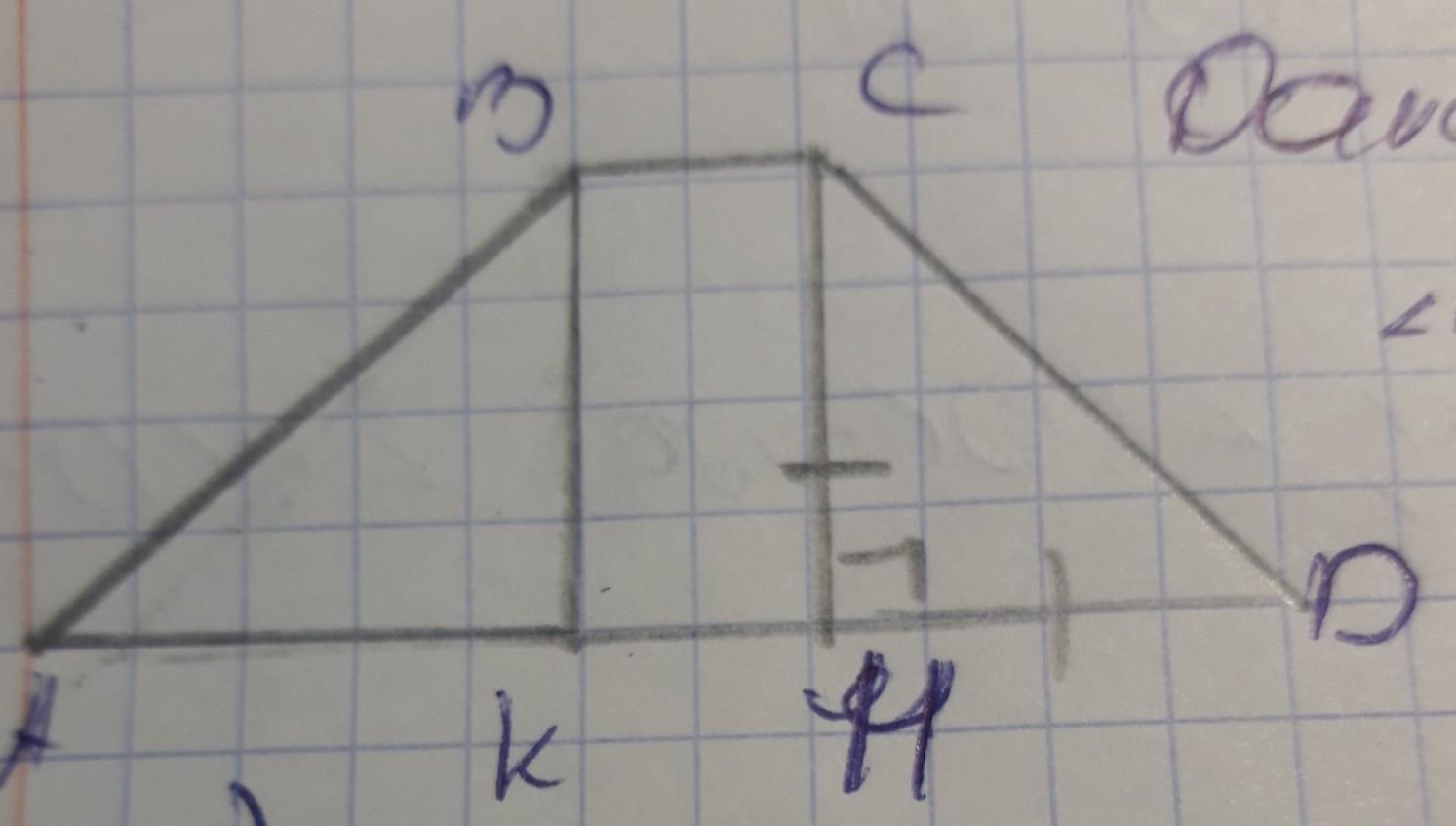
А можете прикрепить чертёж трапеции с двумя высотами СН и ВК?
ок
Ответы
Автор ответа:
1
Пусть ∠ВАК=45°, ∠CDH= 45°, ВС=в , АD=а.
S( трапеции)=1/2*ВК*(АD+ВС).
Ищем высоту.
Обозначим ВК=х. Тогда АК=х , тк прямоугольный ΔАВК- равнобедренный с двумя равными углами по 45° ⇒ СН=х.
ΔСDH- прямоугольный . По свойству угла в 30° , CD=2x. По т Пифагора HD=√((2x)²-x²)=√(3x²)=x√3.
Т. к. с одной стороны AD=a, с другой
AD=АК+КН+НD=х+ВС+ x√3=х+b+ x√3, то
a=x+b+ x√3, a-b=x(1+√3) ,x=(a-b)/(1+√3).
ВК=(a-b)/(1+√3).
S( трапеции)=1/2* (a-b)/(1+√3)*( a+b)=
( a²-b²)/(2(1+√3)).
Избавляясь от иррациональности в знаменателе
( a²-b²)/(2(1+√3))=( a²-b²)* (1-√3)/(-2*2)=
= ( a²-b²)* (-1+√3)/4
Похожие вопросы
Предмет: Русский язык,
автор: Mishcaqueen7
Предмет: Русский язык,
автор: 45453212
Предмет: Русский язык,
автор: tomor
Предмет: Информатика,
автор: Bigdog222
Предмет: Информатика,
автор: dimochka2002voronov