Question

Решите графично уровнение пожайлуста!​

Answer 1

Ответ:

Ответ: (2; 3)

Объяснение:

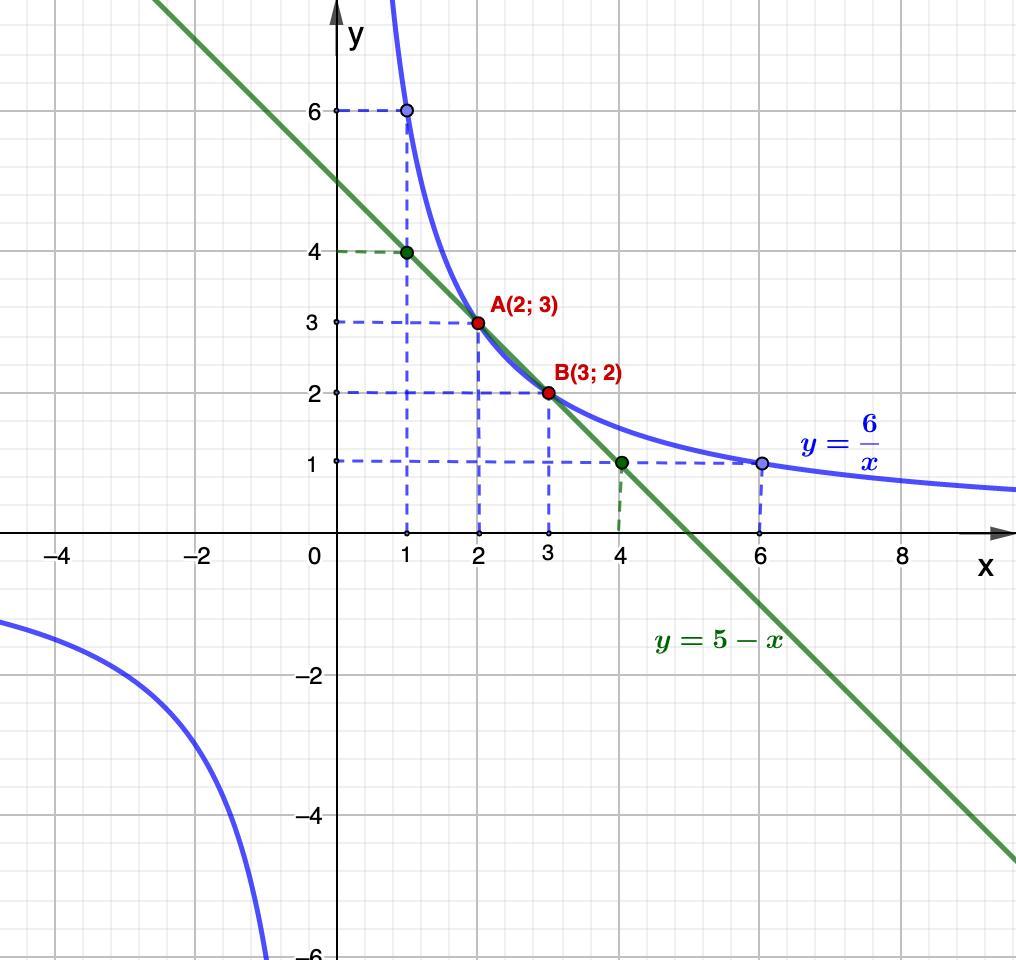
Решить графически уравнение:

$\displaystyle \bf \frac{6}{x} = 5-x$

Построим два графика

$\displaystyle \bf y=\frac{6}{x}\;\;\;u\;\;\;y=5-x$

• Абсциссы точек пересечения этих графиков будут решением данного уравнения.

1.

$\displaystyle \bf y=\frac{6}{x}$

- функция обратной пропорциональности, график - гипербола.

Построим ветвь гиперболы:

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c|c|c| }\cline{1-5}x& 1 & 2 & 3& 6 \\\cline{1-5}y& 6 & 3 & 2& 1 \\\cline{1-5}\end{array}$

Вторую ветвь строим симметрично относительно начала координат.

2.

$\displaystyle \bf y=5-x$

- линейная функция, график - прямая.

Для построения прямой достаточно двух точек:

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c| }\cline{1-3}x& 1 & 4 \\\cline{1-3}y& 4 & 1 \\\cline{1-3}\end{array}$

3. Построили графики.

Точки пересечения:

А (2; 3) и В (3; 2)

Решением уравнения будут абсциссы этих точек пересечения, то есть (2; 3).

Answer 2

Вітаю.

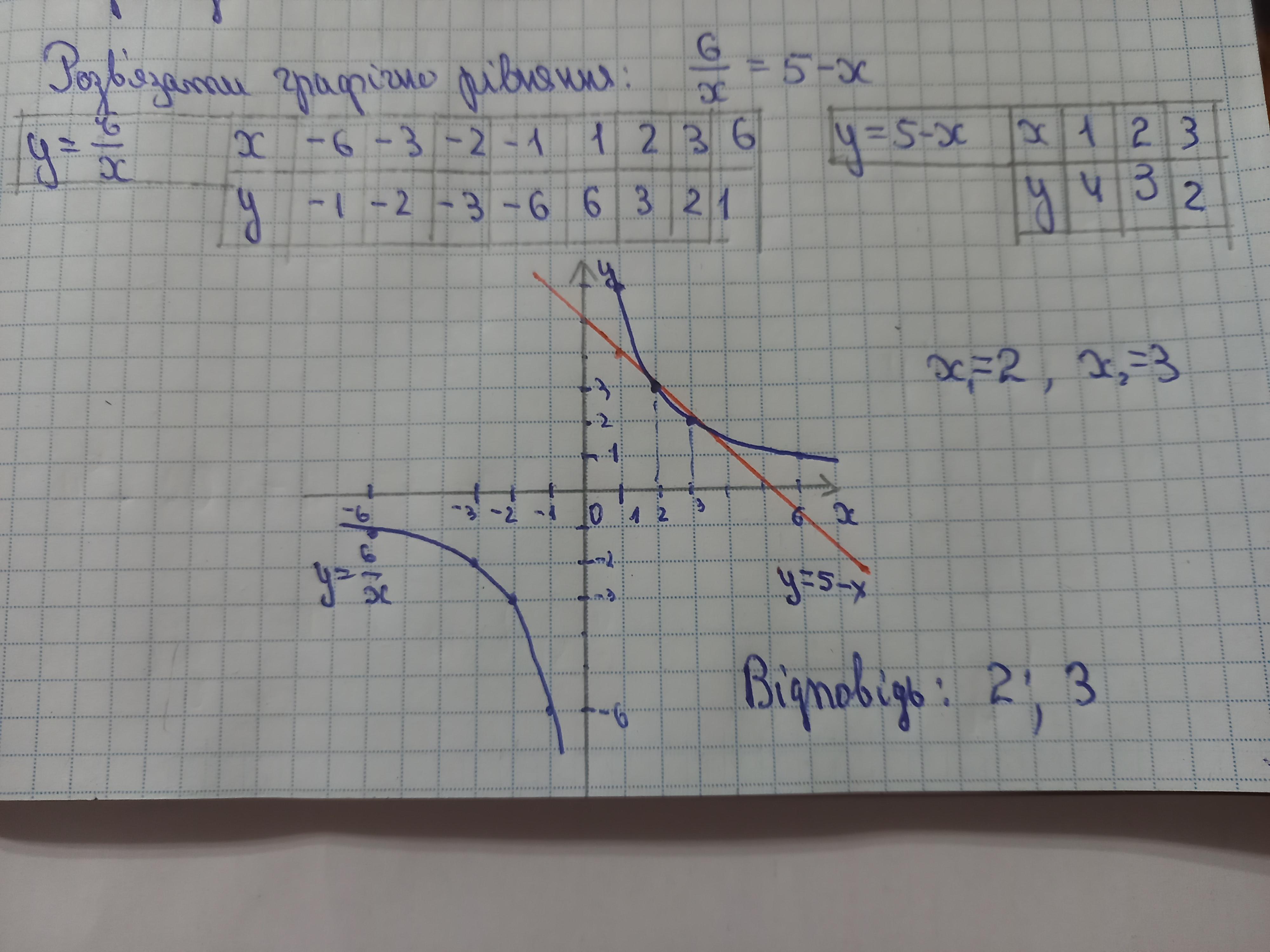
Відповідь: 2; 3.

Розв'язання завдання додаю.

Для побудови прямої достатньо 2 точки, але раджу 3, оскільки при побудові пряма може "з'їхати ". Але це ваш вибір.