Question

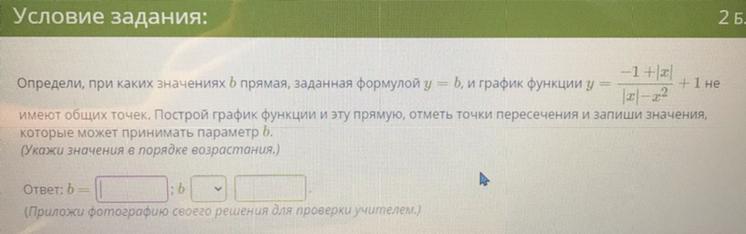
Помогите с алгеброй пж
(Я буду сообщать о спаме так что не отвечайте, если не знаешь ответ)

Answer 1

Ответ:

$b = 0$ или $b \in [1;\,\, + \infty )$

Объяснение:

Упростим выражение, которым задана функция, пользуясь фактом, что ${x^2} = {\left| x \right|^2}$:

$y = \displaystyle\frac{{ - 1 + \left| x \right|}}{{\left| x \right| - {x^2}}} + 1 = \displaystyle\frac{{ - (1 - \left| x \right|)}}{{\left| x \right|(1 - \left| x \right|)}} + 1 = 1 - \displaystyle\frac{1}{{\left| x \right|}},\,\,\left| x \right| \ne 1.$

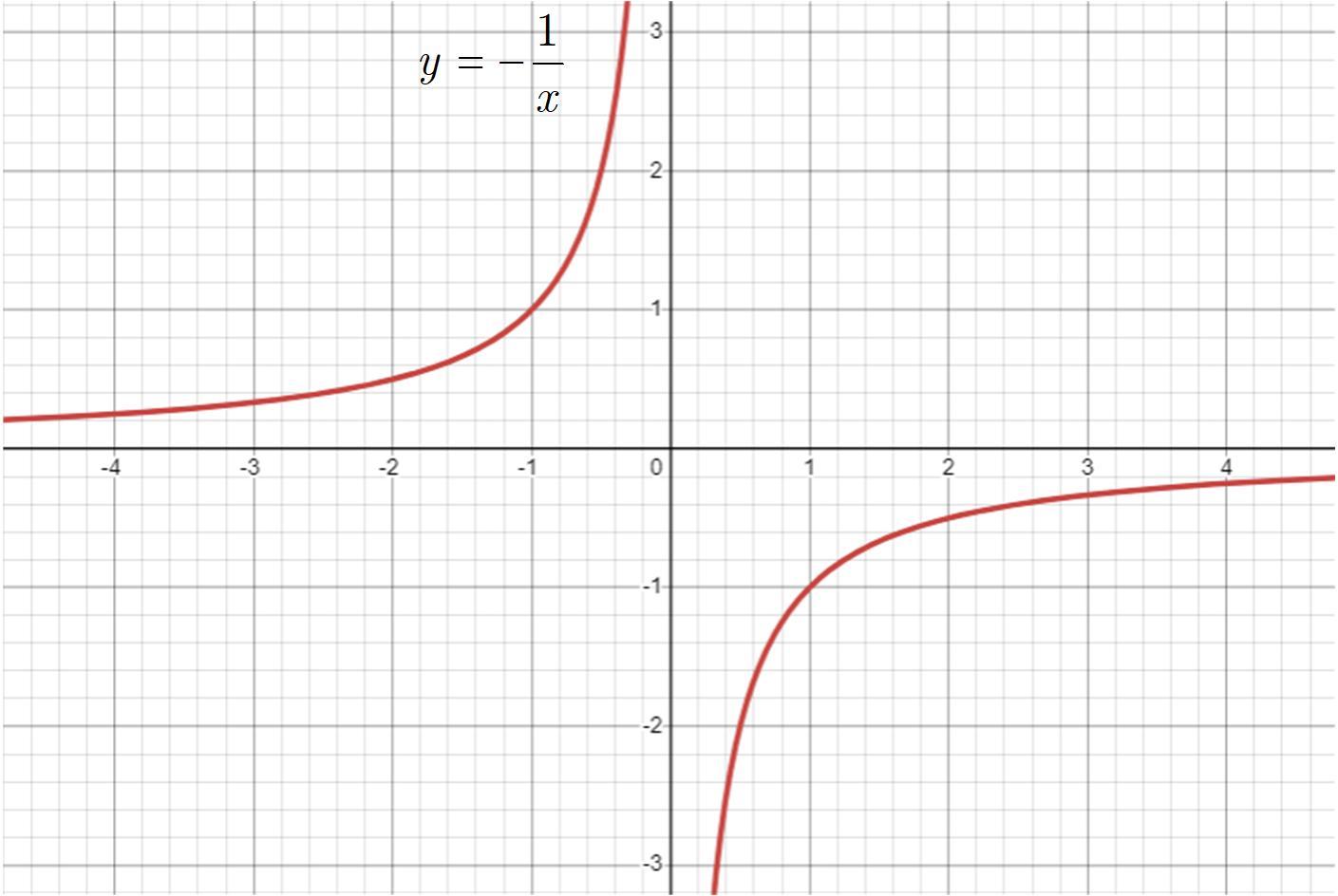
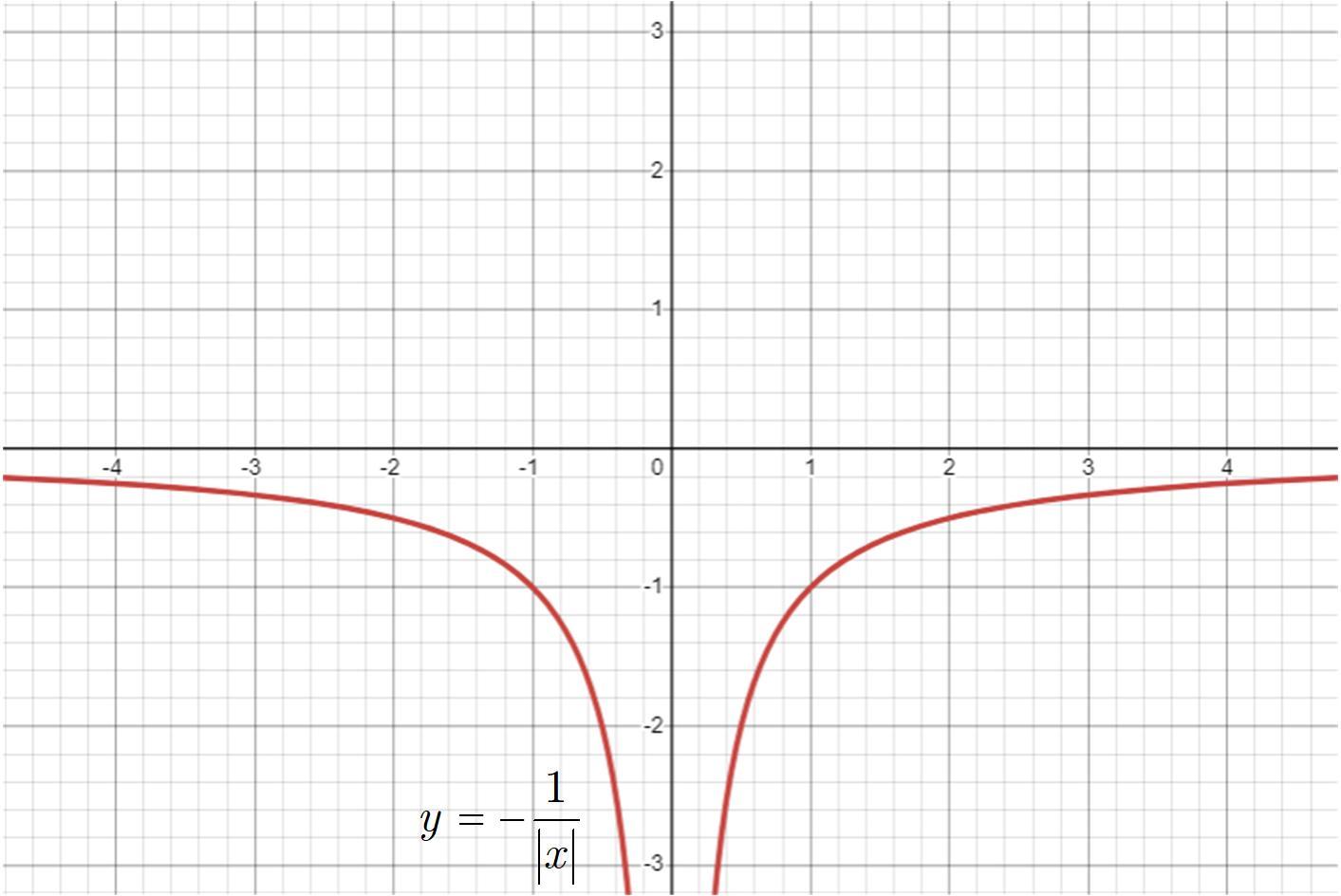
Построение графика функции выполним по следующей схеме:

$y = \displaystyle\frac{1}{x}\,\, \to \,\,y = - \displaystyle\frac{1}{x}\,\, \to \,\,y = - \displaystyle\frac{1}{{\left| x \right|}}\,\, \to \,\,y = 1 - \displaystyle\frac{1}{{\left| x \right|}},$

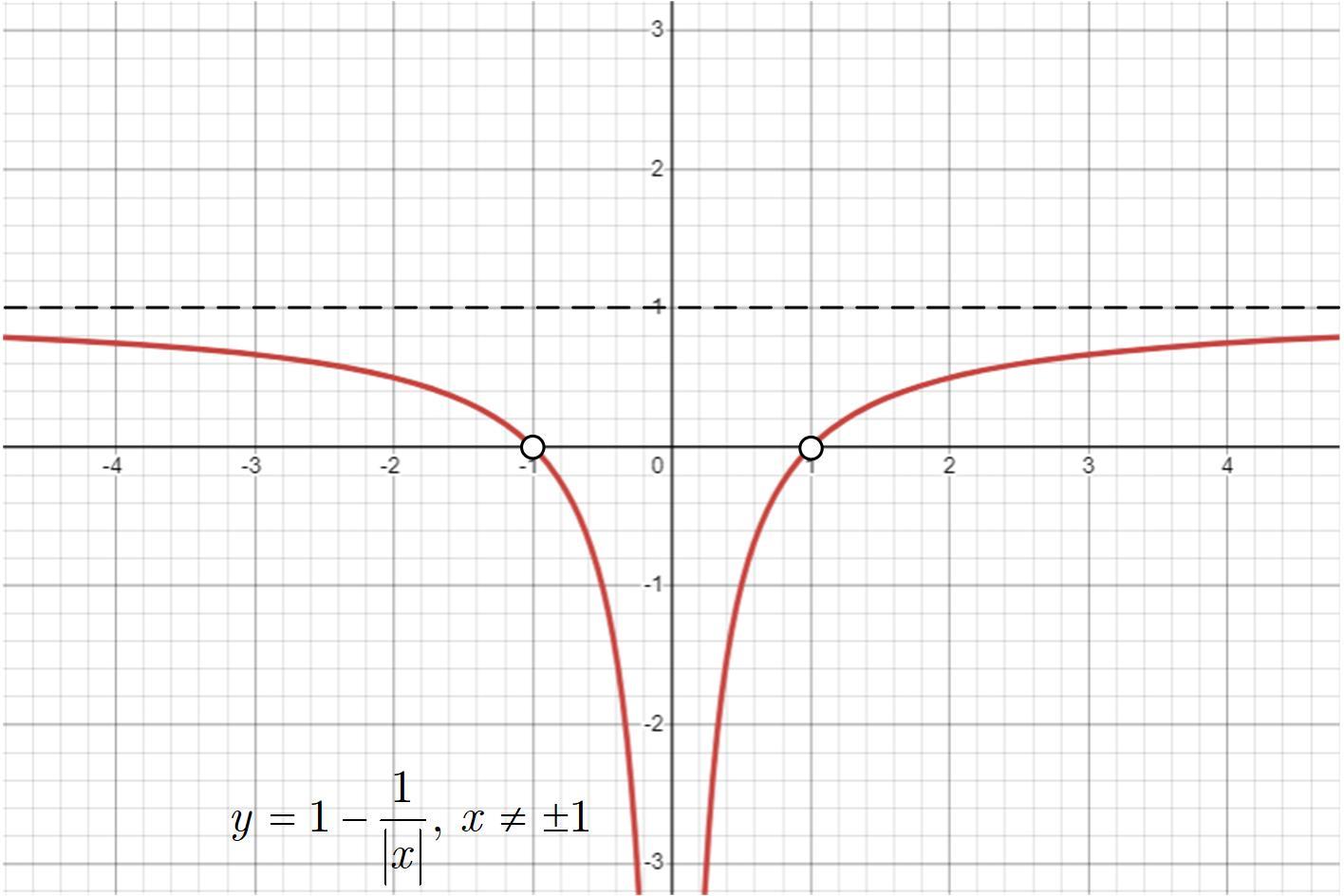
выколем из этого графика точки, соответствующие $\left| x \right| = 1,$ т. е. $x = \pm 1.$

Графиком функции $y = b$ является горизонтальная прямая.

Из последней картинки ясно видно, что графики не будут иметь общих точек при $b = 0$ или $b \in [1;\,\, + \infty ).$