Question

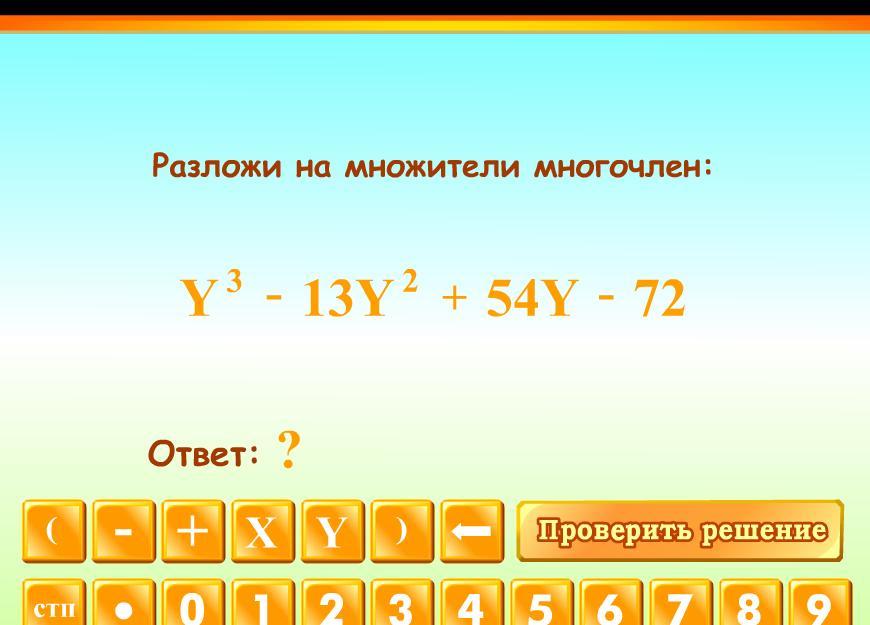
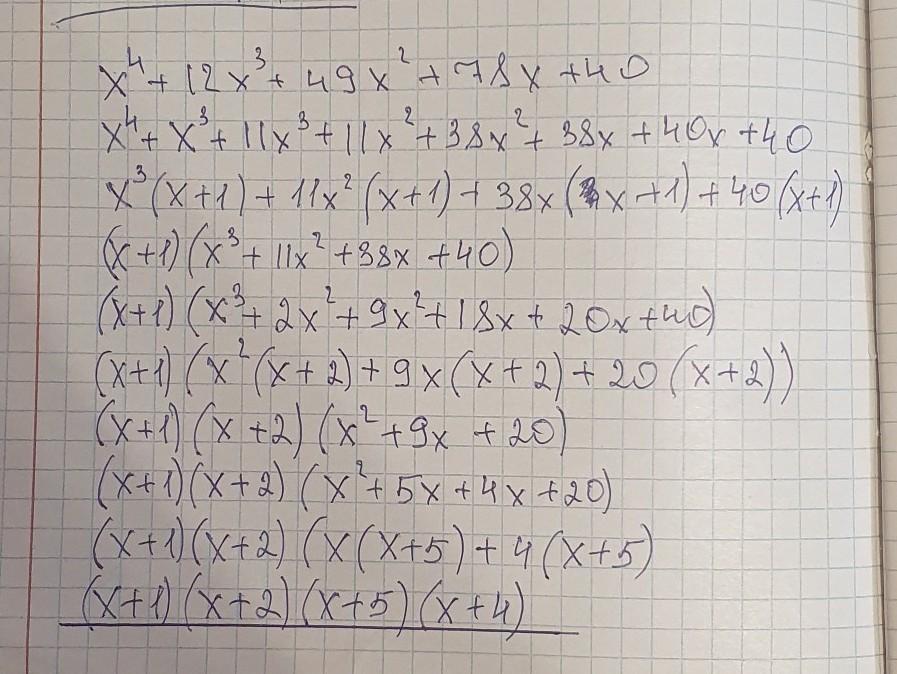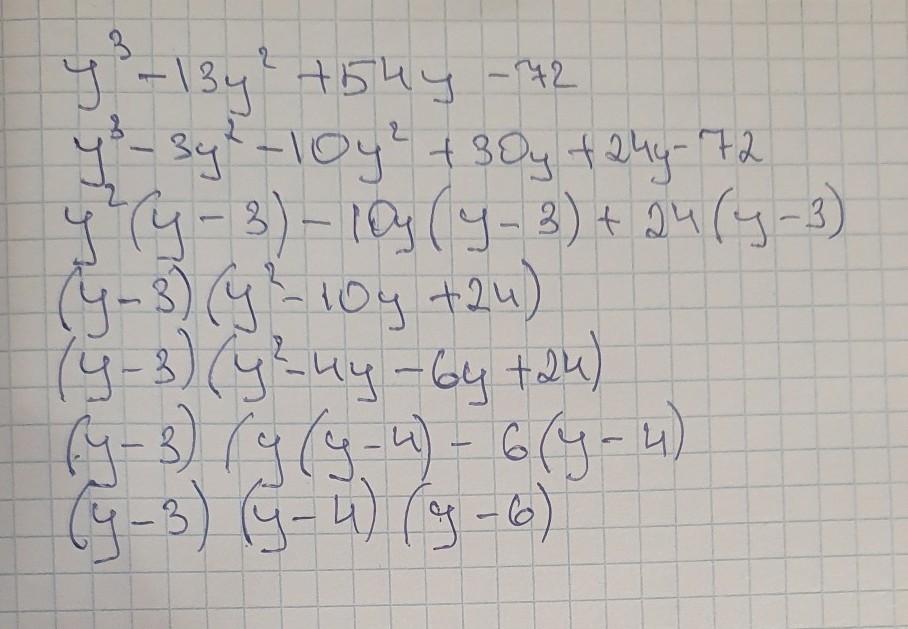Разложи на множители многочлен

Answer 1

Ответ:

1) Подберём первый корень . Он должен находиться среди делителей свободного члена , числа 40 . При подстановке х= -4 в уравнение получим 0 , значит х= -4 - корень многочлена. Значит можно выделить скобку  (х-(-4))=(х+4) .

$x^4+12x^3+49x^2+78x+40=\\\\=(x^4+4x^3)+(8x^3+32x^2)+(17x^2+68x)+(10x+40)=\\\\=x^3(x+4)+8x^2(x+4)+17x(x+4)+10(x+4)=\\\\=(x+4)(x^3+8x^2+17x+10)=$

Опять подбираем корень для многочлена 3 степени среди делителей числа 10 . Это будет х= -5 . И выделяем скобку (х+5) .

$=(x+4)\Big(\, (x^3+5x^2)+(3x^2+15x)+(2x+10)\Big)=\\\\(x+4)\Big(x^2(x+5)+3x(x+5)+2(x+5)\Big)=\\\\=(x+4)(x+4)(x^2+3x+2)=\boldsymbol{(x+4)(x+5)(x+2)(x+1)}\\\\\\\star x^2+3x+2=0\ \ \Rightarrow \ \ x_1=-2\ ,\ x_2=-1\ \ (teorema\ Vieta)\ \ \Rightarrow \\\\x^2+3x+2=(x+2)(x+1)\ \ \star$  

3) Аналогично решаем второй пример. Подбираем первый корень, у=4 и выделяем скобку (х-4) .

$y^3-13y^2+54y-72=(y^3-4y^2)+(-9y^2+36y)+(18y-72)=\\\\=y^2(y-4)-9y(y-4)+18(y-4)=(y-4)(y^2-9y+18)=\\\\=\boldsymbol{(y-4)(y-3)(y-6)}\\\\\star \ \ y^2-9y+18=0\ \ \Rightarrow \ \ y_1=3\ ,\ v_2=6\ \ \ (teorema\ Vieta)\ \ \Rightarrow \\\\y^2-9y+18=(y-3)(y-6)\ \ \star$

Answer 2

Ответ:

(х+1)(х+2)(х+4)(х+5) и (у-3)(у-4)(у-6)

Объяснение:

для облегчения можно разделить число на сумму , а затем вынести отдельно за скобки.

так же во втором при вынесении числа за скобки , возможно , покажется неправильным появление отрицательного числа , но это не так; при произведении двух отрицательных чисел получается положительное.