Предмет: Математика,
автор: littlelove76
Пожалуйста, помогите решить интеграл:
Приложения:
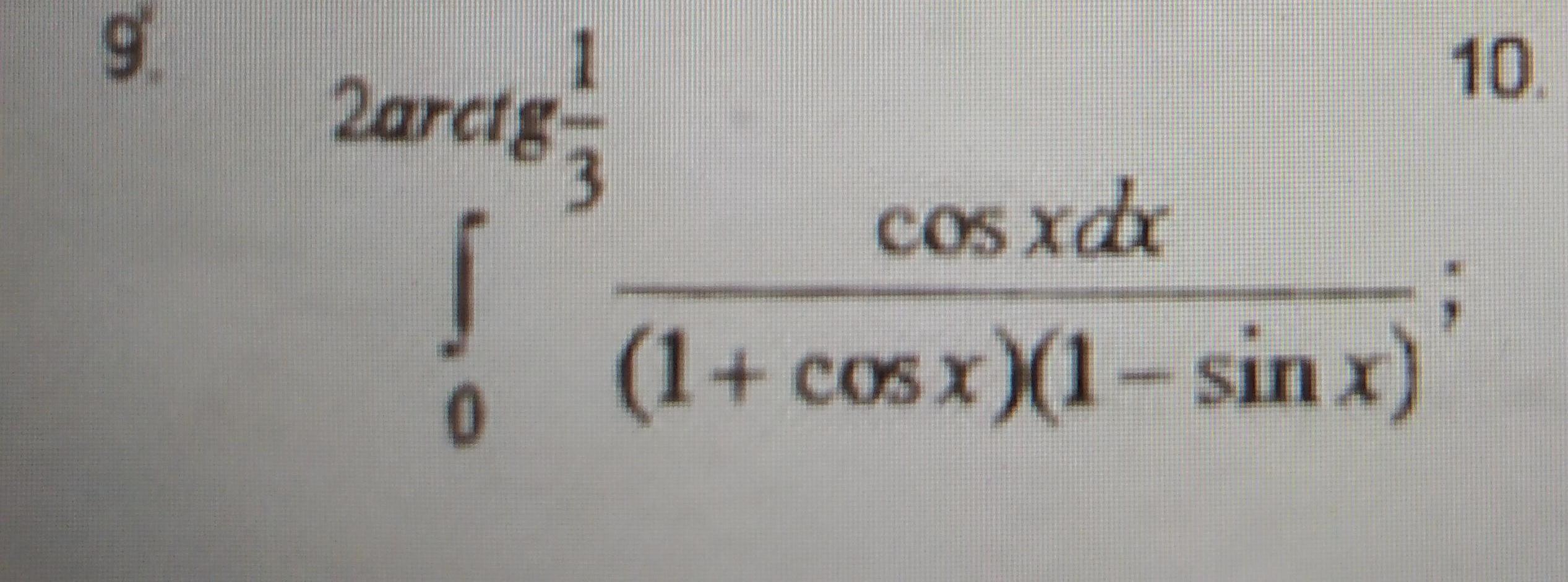
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Воспользуемся универсальной тригонометрической подстановкой. Пусть . Тогда
. Пересчитаем пределы интегрирования:
,
. Получаем:
Похожие вопросы
Предмет: Українська література,
автор: Bodya08
Предмет: Английский язык,
автор: victoriyaruffo1
Предмет: Русский язык,
автор: Mihatiko
Предмет: География,
автор: sixamonjupiter
Предмет: Алгебра,
автор: kolobokpovesilsya