Добрый день.
Прошу помочь с решением задачи.
Найти НОД и НОК многочленов.
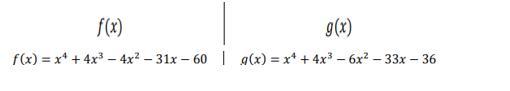
Ответы
Ответ:
НОД(f(x), g(x))=(x-3)(x+4)
НОК(f(x), g(x))=(x-3)(x+4)(x²+3x+5)(x²+3x-+3)
Пошаговое объяснение:
Нужно разложить многочлены на множители.
Ну, т.к. оба многочлена с целыми коэффициентами, то его действительные корни являются делителями свободного члена.
Я их нашел методом подстановки (честно - подставлял в EXCEL).
Оба многочлена имеют по два одинаковых целых корня :
x₁=3; x₂=-4.
Следовательно имеем два одинаковых множителя:
(x-3)*(x+4);
Перемножаем их и получаем:
x²+x-12;
Делим исходные многочлены на полученное выражение любым известным нам способом (например в столбик), получим:
f(x)=x⁴+4x³-4x²-31x-60;
x⁴+4x³-4x²-31x-60 I x²+x-12
x⁴+x³-12x² I x²+3x+5
3x³+8x²-31x
3x³+3x²-36x
5x²+5x-60
5x²+5x-60
0
g(x)=x⁴+4x³-6x²-33x-36
x⁴+4x³-6x²-33x-36 I x²+x-12
x⁴+x³-12x² I x²+3x+3
3x³+6x²-33x
3x³+3x²-36x
3x ²+3x-36
3x ²+3x-36
0
Получаем разложение на множителио такое:
f(x)=(x²+x-12)*(x²+3x+5-)=(x-3)(x+4)(x²+3x+5);
g(x)=(x²+x-12*)(x²+3x-12)=(x-3)(x+4)(x²+3x+3)
На множестве действительных чисел "лучше" не разложишь, т.к. корни квадратных трехчленов комплексные.
Ну и теперь:
НОД(f(x), g(x))=(x-3)(x+4);
НОК(f(x), g(x))=(x-3)(x+4)(x²+3x+5)(x²+3x+3).