Предмет: Геометрия,
автор: ipodolna08
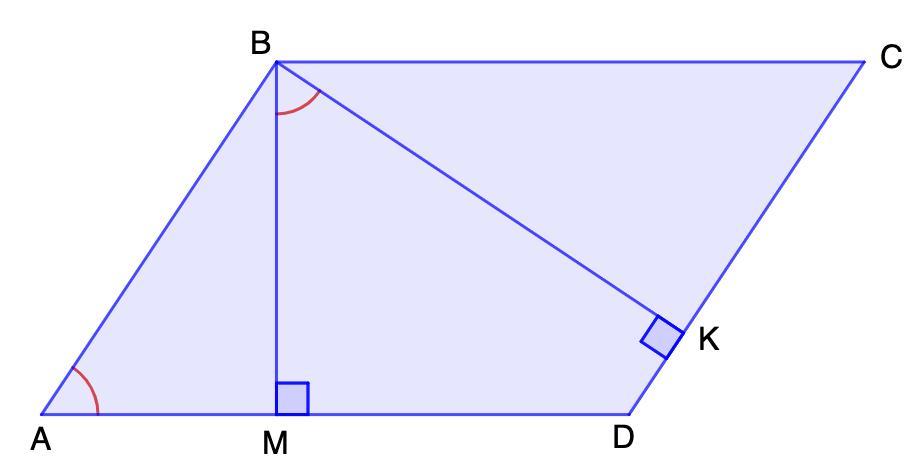
5. У паралелограмі ABCD з вершини тупого кута в проведено висоти BM i ВК. Доведіть, що кути МВК i BAD рівні.
Ответы
Автор ответа:
3
Ответ:
Доказано, что ∠BAD = ∠МВК.
Объяснение:
5. В параллелограмме ABCD из вершины тупого угла в проведены высоты BM и ВК. Докажите, что углы МВК и BAD равны.
Дано: ABCD - параллелограмм;
BM и ВК - высоты.
Доказать: ∠МВК = ∠BAD.
Доказательство:
- Углы параллелограмма, прилежащие к одной стороне. в сумме равны 180°.
⇒ ∠BAD = 180° - ∠D (1).
Рассмотрим МВКD.
Сумма углов четырехугольника равна 360°.
⇒ ∠МВК + ∠ВКD + ∠D + ∠BMD = 360°
∠ВКD = 90° (BK - высота)
∠BMD = 90° (ВМ - высота)
⇒ ∠МВК + 90° + ∠D + 90° = 360°
или
∠МВК + ∠D = 180°
То есть:
∠МВК = 180° - ∠D (2).
У равенств (1) и (2) правые части равны, значит равны и левые.
⇒ ∠BAD = ∠МВК
Доказано, что ∠BAD = ∠МВК.
Приложения:
Автор ответа:
5
Доброї, спокійної ночі.
Доведення, 2 способи.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: a4help
Предмет: Русский язык,
автор: Zagadochnaya
Предмет: Русский язык,
автор: ХубиеваК5
Предмет: Математика,
автор: qwerty27064
Предмет: Українська мова,
автор: telefon5331s
https://znanija.com/task/49786554